Formule de calcul de laire latérale dun cône tronqué, de laire totale dun cône tronqué, du volume dun cône tronqué

Nous vous invitons à découvrir ce qu'est un cône tronqué, la formule de calcul du volume d'un cône tronqué, l'aire latérale et l'aire totale d'un cône tronqué dans l'article ci-dessous.

Comme nous l'avons appris dans l'article précédent, une pyramide se forme lorsqu'un triangle rectangle est tourné autour de son axe (un côté à angle droit) d'un tour.

cône tronqué

• 1. Calculer l'aire d'un cône tronqué
  • 1.1. Calculer l'aire latérale d'un cône tronqué
  • 1.2. Calculer l'aire totale d'un cône tronqué
• 2. Calculer le volume d'un cône tronqué
• Qu'est-ce qu'un cône tronqué ?

1. Calculer l'aire d'un cône tronqué

L'aire d'un cône tronqué est souvent désignée par deux concepts : l'aire latérale et l'aire totale.

1.1. Calculer l'aire latérale d'un cône tronqué

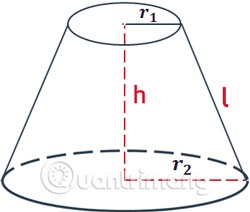
Là-dedans :

• Le périmètre est la zone autour du cône tronqué.
• r1et r2est le rayon des deux bases du cône tronqué.
• lest la longueur de la génératrice du tronc de cône.

L'aire latérale d' un cône tronqué comprend uniquement l'aire des faces environnantes entourant le cône, sans compter l'aire des deux bases.

Formule de calcul de l'aire latérale : égale à la différence d'aire latérale du grand cône et du petit cône.

1.2. Calculer l'aire totale d'un cône tronqué

• r1et r2est le rayon des deux bases du cône tronqué.
• lest la longueur de la génératrice du tronc de cône.

Ainsi:

Là-dedans :

• La zone autour d'un cône tronqué est la zone qui l'entoure.
• Le stoalphan est la surface totale d'un cône tronqué.
• S2day est l'aire des 2 surfaces inférieures

L'aire totale est calculée comme la grandeur de l'espace entier occupé par la figure, y compris l'aire latérale et l'aire des deux bases circulaires.

Formule de calcul de l'aire totale : égale à l'aire latérale plus l'aire de 2 bases.

Par exemple:

Étant donné un cône tronqué avec des rayons de base r1 et r2 égaux respectivement à 5 cm et 7 cm. La ligne génératrice reliant le sommet à la base du cône mesure 6 cm. Quelle est l'aire totale et l'aire latérale de ce cône ?

Prix:

En appliquant la formule de calcul de l'aire totale d'un cône tronqué, nous avons r1 = 5cm, r2 = 7cm et la longueur du générateur l = 6cm. Déduire l'aire totale d'un cône tronqué en appliquant la formule suivante :

Stp = π.(5 + 7).4 + (π.52 + π.72) = π.12.4 + (π.25 + π.49) = 383.08 (cm2).

Ainsi, la surface totale de ce cône tronqué est d'environ 383,08 cm2.

L'aire latérale d'un cône tronqué est :

Sxq = π.(r1 + r2).l = π.(5 +7).6 ~ 226 cm2.

2. Calculer le volume d'un cône tronqué

Le volume d'un tronc de cône est la quantité d'espace qu'il occupe.

Formule de calcul du volume d'un cône tronqué : égal à la différence de volume du grand cône et du petit cône.

Là-dedans :

• Vest le volume du cône tronqué.
• r1et r2est le rayon des deux bases du cône tronqué.
• hest la hauteur du cône tronqué (distance entre les 2 bases).

Par exemple : Soit un cône tronqué dont les rayons de base r1 et r2 sont respectivement égaux à 5 cm et 9 cm. La hauteur reliant les deux rayons de base est de 8 cm de long. Quelle est la surface totale de ce cône ?

Prix: 

En appliquant la formule de calcul du volume d'un cône tronqué, nous avons : r1 = 5cm, r2 = 9cm, h = 8cm.
V = 1/3π.8. (52 + 5,9 +92) = 1264,37 (cm3).

Ainsi, le volume de ce cône tronqué est d'environ 1264,367 cm3.

Exemple 2 :

Étant donné un cône tronqué comme indiqué sur la figure.

Sachant que le rayon de la petite base est r = 3cm, le rayon de la grande base est R = 6cm, longueur AB = 4cm. Calculez l'aire latérale et le volume du cône tronqué.

Prix:

L'aire latérale d'un cône tronqué est :

Sxq = π(r + R)l = π(3 + 6).4 = 36π (cm2)

Pour calculer la hauteur d'un cône tronqué, nous avons le dessin suivant :

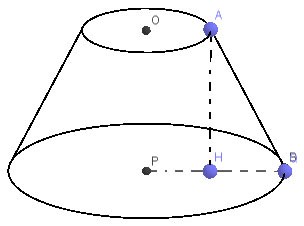
En appliquant le théorème de Pythagore et le triangle rectangle AHB en H, nous avons :

Le volume d'un cône tronqué est :

• Formule de calcul du volume d'une pyramide tronquée, de l'aire latérale et de l'aire totale d'une pyramide tronquée

Qu'est-ce qu'un cône tronqué ?

Lorsqu'un cône est coupé par un plan parallèle à la base, la partie du plan à l'intérieur du cône est un cercle . La partie de la forme entre le plan ci-dessus et la base est appelée un cône tronqué.

On peut comprendre qu'un cône tronqué est une forme avec deux bases qui sont deux cercles de rayons différents situés sur deux plans parallèles avec la ligne reliant les centres comme axe de symétrie.

Vous pouvez facilement voir que nous rencontrons souvent des cônes tronqués dans la vie tels que des seaux ou des abat-jour... J'espère que grâce à l'article ci-dessus, vous avez une meilleure compréhension des cônes tronqués et comment calculer l'aire et le volume des cônes tronqués.