Formule de calcul de laire dun triangle : rectangle, régulier, isocèle, équilatéral

Quelle est la formule pour calculer l'aire d'un triangle régulier, rectangle et isocèle ? Veuillez vous référer à l'article ci-dessous pour comprendre les méthodes les plus simples et les plus couramment utilisées pour calculer l'aire d'un triangle.

Table des matières

• 1. Calculer l'aire d'un triangle régulier
• 2. Calculer l'aire d'un triangle isocèle
• 3. Calculer l'aire d'un triangle équilatéral
• 4. Calculer l'aire d'un triangle rectangle
• 5. Calculer l'aire d'un triangle rectangle isocèle
• 6. Formule de calcul de l'aire d'un triangle dans le système de coordonnées Oxyz
• Types de triangles

1. Calculer l'aire d'un triangle régulier

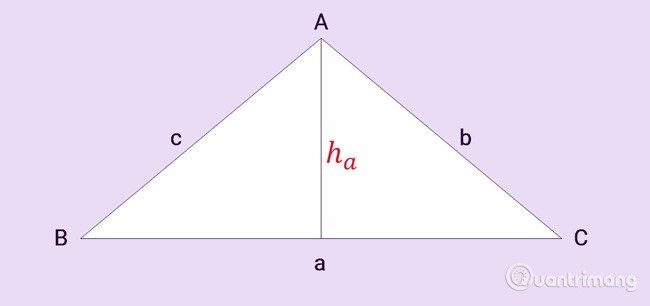
Le triangle ABC a trois côtés a, b, c, ha est la hauteur du sommet A comme indiqué :

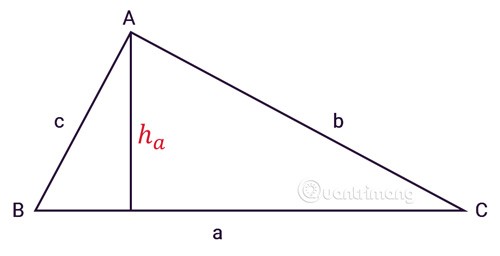
un. Formule générale

L'aire d'un triangle est égale à la hauteur multipliée par la longueur du côté opposé (la base) et divisée par 2.

Poème sur le calcul de l'aire d'un triangle régulier

L'aire d'un triangle est facile.
Multipliez la hauteur par la base et divisez-la en deux.

Par exemple:

Calculer l'aire d'un triangle dont la base mesure 5 m et la hauteur 24 dm.

Solution : Hauteur 24dm = 2,4 m

L'aire du triangle est :

b. Calculer l'aire d'un triangle lorsqu'un angle est connu

L'aire d'un triangle est égale à la moitié du produit de deux côtés adjacents multiplié par le sinus de l'angle entre ces deux côtés du triangle.

Par exemple:

Le triangle ABC a le côté BC = 7, le côté AB = 5, l'angle B est égal à 60 degrés. Calculer l'aire du triangle ABC ?

Prix:

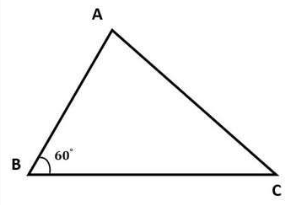
c. Calculer l'aire d'un triangle en connaissant 3 côtés à l'aide de la formule de Heron.

En utilisant la formule éprouvée Heron :

Avec p étant le demi-périmètre du triangle :

Peut être réécrit en utilisant la formule :

Par exemple:

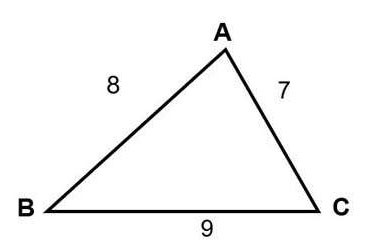
Calculer l'aire du triangle dont les côtés sont AB = 8, AC = 7, CB = 9

Prix:

Le demi-périmètre du triangle ABC est

En appliquant la formule du héros, nous avons

d. Calculez l'aire par le rayon du cercle circonscrit au triangle (R).

Autre:

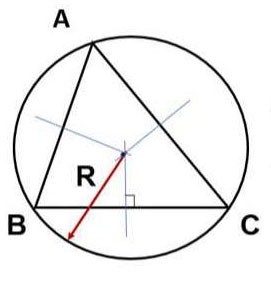
Remarque : Il est nécessaire de prouver que R est le rayon du cercle circonscrit au triangle.

Par exemple:

Étant donné le triangle ABC, les longueurs des côtés a = 6, b = 7, c = 5, R = 3 (R est le rayon du cercle circonscrit au triangle ABC). Calculer l'aire du triangle ABC.

Prix:

f. Calculez l'aire en utilisant le rayon du cercle inscrit dans le triangle (r).

• p : La moitié du périmètre du triangle.
• r : Rayon du cercle inscrit.

Par exemple : Calculer l'aire du triangle ABC connaissant les longueurs des côtés AB = 20, AC = 21, BC = 15, r = 5 (r est le rayon du cercle inscrit dans le triangle ABC).

Prix:

Le demi-périmètre d'un triangle est :

r= 5

L'aire du triangle est :

2. Calculer l'aire d'un triangle isocèle

Les triangles isocèles sont comme des triangles réguliers, nous pouvons appliquer la formule consistant à multiplier la hauteur par la base, puis à diviser par 2 comme ci-dessus. Il y aura également des formules avancées plus complexes :

Le triangle isocèle ABC a trois côtés, a est la longueur de la base, b est la longueur des deux côtés, ha est la hauteur à partir du sommet A comme indiqué :

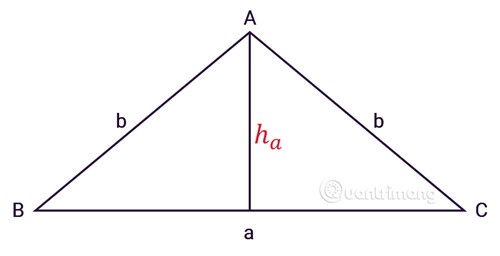
En appliquant la formule de calcul de l'aire d'un triangle régulier, nous avons la formule de calcul de l'aire d'un triangle isocèle :

3. Calculer l'aire d'un triangle équilatéral

Le triangle équilatéral ABC a trois côtés égaux, a est la longueur des côtés comme indiqué :

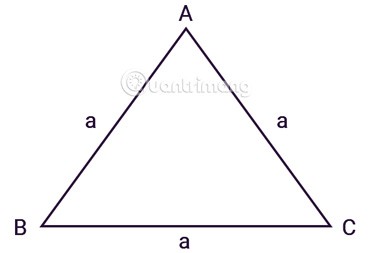
En appliquant le théorème de Heron pour déduire, nous avons la formule pour calculer l'aire d'un triangle équilatéral :

4. Calculer l'aire d'un triangle rectangle

Le triangle ABC est rectangle en B, a, b sont les longueurs des deux côtés rectangles :

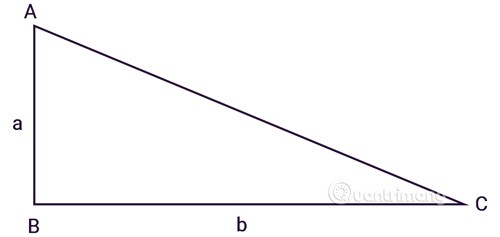
Appliquez la formule pour calculer l'aire d'un triangle rectangle dont la hauteur est l'un des deux côtés de l'angle droit et la base est le côté restant.

Formule pour calculer l'aire d'un triangle rectangle :

Poème sur le calcul de l'aire d'un triangle rectangle :

Triangle avec deux angles droits.
Restez calme, ne paniquez pas et ne faites pas d’erreurs.

Côté, côté multiplié, divisé par deux
est la surface, faites l'exercice rapidement

5. Calculer l'aire d'un triangle rectangle isocèle

Le triangle ABC est un triangle rectangle en A, a est la longueur des deux côtés :

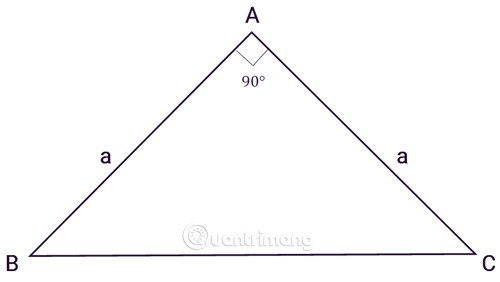
En appliquant la formule de calcul de l'aire d'un triangle rectangle à l'aire d'un triangle rectangle isocèle de hauteur et de base égales, on obtient la formule :

6. Formule de calcul de l'aire d'un triangle dans le système de coordonnées Oxyz

Théoriquement, nous pouvons utiliser les formules ci-dessus pour calculer l'aire d'un triangle dans l'espace ou dans l'espace Oxyz. Cependant, cela entraînera quelques difficultés de calcul. Par conséquent, dans l'espace Oxyz, les gens calculent souvent l'aire d'un triangle en utilisant le produit directionnel.

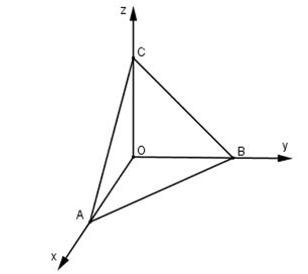
Dans l'espace Oxyz, étant donné le triangle ABC. L'aire du triangle ABC est calculée par la formule :

Exemple :

Dans l'espace Oxyz, le triangle ABC est donné avec les coordonnées de trois sommets A(-1;1;2), B(1;2;3), C(3;-2;0). Calculer l'aire du triangle ABC.

Solution :

Nous avons:

Pour calculer l'aire d'un triangle, vous devez déterminer de quel type de triangle il s'agit, à partir de là trouver la formule de calcul d'aire correcte et les facteurs nécessaires pour calculer l'aire d'un triangle le plus rapidement possible.

Types de triangles

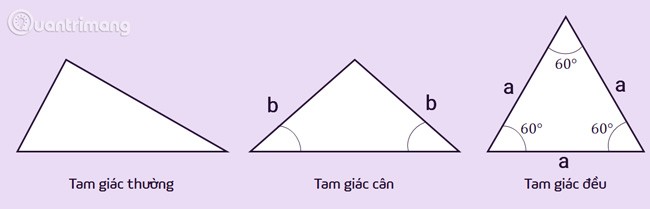
Triangle régulier : c'est le triangle le plus basique, il a différentes longueurs de côté et différentes mesures d'angle intérieur. Les triangles réguliers peuvent également inclure des cas particuliers de triangles.

Triangle isocèle : est un triangle avec deux côtés égaux, ces deux côtés sont appelés les deux côtés latéraux. Le sommet d'un triangle isocèle est l'intersection de deux côtés adjacents. L'angle formé par le sommet est appelé angle au sommet, les deux autres angles sont appelés angles à la base. La propriété d'un triangle isocèle est que les deux angles à la base sont égaux.

Triangle équilatéral : est un cas particulier de triangle isocèle dont les trois côtés sont égaux. La propriété d'un triangle équilatéral est qu'il a 3 angles égaux et mesure 60 degrés.

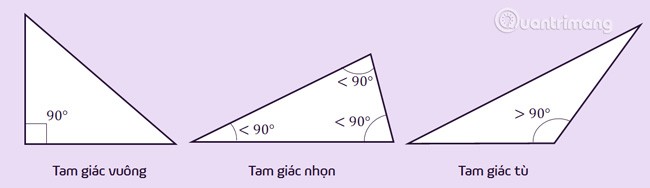
Triangle rectangle : est un triangle dont un angle est égal à 90 (un angle droit).

Triangle obtus : est un triangle avec un angle intérieur supérieur à 90 (un angle obtus) ou un angle extérieur inférieur à 90 (un angle aigu).

Triangle aigu : est un triangle avec trois angles intérieurs tous inférieurs à 90 (trois angles aigus) ou avec tous les angles extérieurs supérieurs à 90 (six angles obtus).

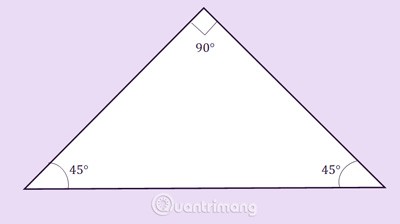
Triangle rectangle isocèle : est à la fois un triangle rectangle et un triangle isocèle.

• Formule de calcul du périmètre d'un triangle
• Formule de calcul de la hauteur dans les triangles réguliers, isocèles, équilatéraux et rectangles
• Quel est l'objectif ? Formule de calcul du centre de gravité d'un triangle
• Qu'est-ce qu'une bissectrice perpendiculaire ?

Ci-dessus se trouve un résumé des formules courantes de calcul de l'aire d'un triangle, calculant l'aire d'un triangle dans le système de coordonnées oxyz. Si vous avez des préoccupations, des questions ou des contributions, veuillez laisser un commentaire ci-dessous pour en discuter avec Quantrimang.com.