Système décimal (base 10)
Le système numérique décimal est le système standard et le plus couramment utilisé dans la vie quotidienne. Ce système de comptage utilise le nombre 10 comme base. Le système décimal se compose de 10 caractères, qui sont les nombres de 0 à 9. Plus précisément 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
En tant que l’un des plus anciens systèmes numériques connus, le système numérique décimal était utilisé par de nombreuses civilisations anciennes. La difficulté de représenter de très grands nombres dans le système décimal a été surmontée par le système numérique hindou-arabe. Le système numérique hindou-arabe fournit des positions pour les chiffres dans un nombre. Chaque position équivaut à une puissance de 10, en commençant par la position la plus à droite avant la virgule décimale qui est 100.
Par exemple, le nombre 2345,67 en décimal :
Par conséquent, le nombre 2345,67 peut également être représenté comme : (2 * 103) + (3 * 102) + (4 * 101) + (6 * 10-1) + (7 * 10-2).
Exemple de conversion de la base 10 en base 16 :
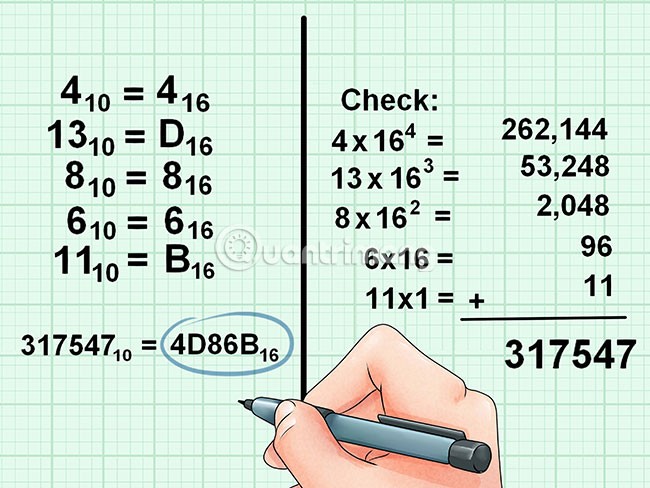
Hexadécimal (base 16)
Le système numérique hexadécimal, Hex ou hexadécimal utilise un système numérique de base 16 et constitue un choix populaire pour représenter de longues valeurs binaires, car leur format est beaucoup plus compact et plus facile à comprendre que les longues chaînes binaires composées uniquement de 2 valeurs 1 et 0.
Tableau de conversion de la base 10 à la base 16
| Système de base 10 | Système hexadécimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | UN |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
Voir aussi :
Craving for snacks but afraid of gaining weight? Dont worry, lets explore together many types of weight loss snacks that are high in fiber, low in calories without making you try to starve yourself.
Vous rencontrez des problèmes avec le proxy dans Microsoft Teams ? Découvrez des solutions éprouvées pour résoudre ces erreurs. Videz le cache, ajustez les paramètres du proxy et retrouvez des appels fluides en quelques minutes grâce à notre guide expert.
Vous êtes frustré(e) car votre enregistrement Microsoft Teams a échoué ? Découvrez les principales causes, telles que les problèmes d’autorisation, les limites de stockage et les dysfonctionnements du réseau, ainsi que des solutions étape par étape pour éviter les échecs futurs et enregistrer parfaitement à chaque fois.
Vous êtes frustré(e) car les salles de sous-groupes sont introuvables dans vos réunions Teams ? Découvrez les principales raisons de leur absence et suivez nos solutions pas à pas pour les activer en quelques minutes. Idéal pour les organisateurs comme pour les participants !
Vous rencontrez des problèmes avec le Trousseau d'accès Microsoft Teams sur Mac ? Découvrez des solutions de dépannage éprouvées et détaillées pour macOS afin de retrouver une collaboration fluide. Des solutions rapides à l'intérieur !
Découvrez l'emplacement précis des clés de registre Microsoft Teams sous Windows 11. Ce guide pas à pas vous explique comment les trouver, y accéder et les modifier en toute sécurité pour optimiser les performances et résoudre les problèmes. Indispensable pour les professionnels de l'informatique et les utilisateurs de Teams.
Vous en avez assez de l'erreur 1200 de Microsoft Teams qui interrompt vos appels téléphoniques ? Découvrez des solutions rapides et simples pour iOS et Android afin de reprendre rapidement une collaboration fluide, sans aucune compétence technique requise !
Vous êtes frustré(e) par la disparition de l'icône Microsoft Teams dans Outlook ? Découvrez où la trouver, pourquoi elle disparaît et comment la faire réapparaître pour des réunions sans souci. Mise à jour pour les dernières versions !
Vous rencontrez des difficultés avec le chargement des onglets Wiki dans Microsoft Teams ? Découvrez des solutions éprouvées, étape par étape, pour résoudre rapidement le problème, restaurer vos onglets Wiki et optimiser la productivité de votre équipe en toute simplicité.
Vous en avez assez des plantages de Microsoft Teams avec erreur critique ? Découvrez la solution éprouvée de 2026 modifications du registre qui résout le problème en quelques minutes. Guide pas à pas, captures d'écran et astuces pour une solution définitive. Compatible avec les dernières versions !
