Apprenons la formule de calcul de l'aire latérale, de l'aire totale et de la hauteur d'un cylindre à appliquer dans les études et la vie quotidienne.
Table des matières
Comment calculer l'aire d'un cylindre
L'aire d'un cylindre comprend l'aire latérale et l'aire totale.
Vous pouvez saisir la hauteur et le rayon du cylindre dans le tableau ci-dessous pour connaître la surface latérale et la surface totale du cylindre.
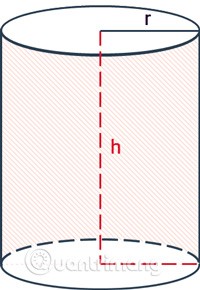
Formule de calcul de l'aire latérale d'un cylindre
L'aire latérale d'un cylindre comprend uniquement l'aire de la surface environnante entourant le cylindre, sans compter l'aire des deux bases.
La formule de calcul de l'aire latérale d'un cylindre est la circonférence du cercle de base multipliée par la hauteur.
 |
Là-dedans :
- Les environs sont les environs.
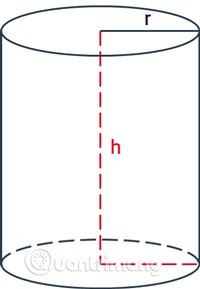
rest le rayon du cylindre.hest la hauteur, la distance entre les deux bases du cylindre.
|
Exemple : 1
Un cylindre circulaire a un rayon de base r = 5 cm et une hauteur h = 7 cm. Calculer l'aire latérale d'un cylindre vertical.
Solution : Aire de surface d'un cylindre circulaire : Sxq = 2.π.rh = 2π.5,7 = 70π = 219,8 (cm2).
Exemple : 2
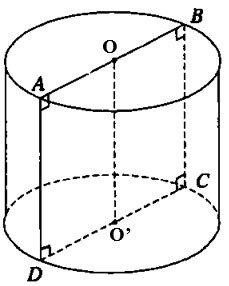
Étant donné le carré ABCD de côté 2a. Soient O et O' les milieux des côtés AB et CD respectivement. En faisant tourner ce carré autour de l'axe OO', on obtient un cylindre en rotation. Calculer l'aire de la surface du cylindre en rotation.
Solution:
Le rayon du cercle de base est r= CD= a
La hauteur du cylindre est h= OO'= AD=2a
Donc l'aire latérale du cylindre est Sxq = 2πrh = 2π.a.2a =4a2π
Formule de calcul de l'aire totale d'un cylindre
L'aire totale est calculée comme la grandeur de l'espace entier occupé par la figure, y compris l'aire latérale et l'aire des deux bases circulaires.
La formule pour calculer l'aire totale d'un cylindre est l'aire latérale plus l'aire des deux bases.
Exemple 1 : Calculer l'aire totale d'un cylindre de base 3 et de hauteur 5.
Solution:
La surface totale est Stp= Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) =48π
Calculer la hauteur du cylindre
La hauteur d'un cylindre est la distance entre les deux bases du cylindre.
Calculer la hauteur d'un cylindre en connaissant la surface totale et le rayon de la base
Par exemple : Soit un cylindre avec un rayon de base R = 8 cm et une surface totale de 564π cm2. Calculer la hauteur du cylindre.
Prix:
Nous avons
Calculer la hauteur d'un cylindre en connaissant l'aire latérale
=>
Formule de calcul du rayon de la base d'un cylindre
1. Formule pour calculer la circonférence d'un cercle ; aire du cercle
Le cercle a une circonférence C=2πr
=>
Le cercle avec la base a une aire S=πr2
=>
Par exemple. Calculez le rayon de la base du cylindre dans les cas suivants :
un. La circonférence du cercle de base est de 6π
b. L'aire de la base est de 25π
Solution:
un. Le rayon du cercle de base est
b. Le rayon du cercle de base est
2. La base est le cercle inscrit dans le polygone
- Inscrit dans un triangle quelconque : avec S étant l'aire du triangle et p étant le demi-périmètre
- Inscrit dans un triangle équilatéral : côté
- Carré inscrit :
Exemple 1 . Étant donné un cylindre inscrit dans un cube d'arête a. Calculez le rayon de ce cylindre.
Le rayon du cylindre est :
Exemple 2 . Étant donné un prisme régulier ABC.A'B'C' avec , le volume circonscrit au cylindre. Calculez le rayon de ce cylindre.
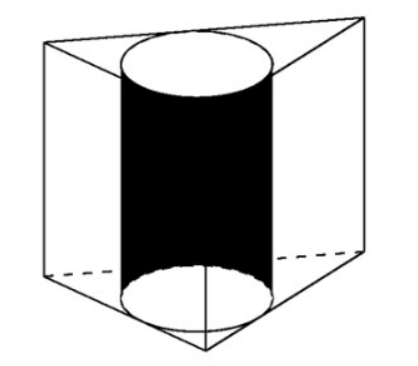
Le volume du prisme est
La base d'un prisme régulier est un triangle équilatéral, donc => le côté
Par conséquent, le rayon de la base du cylindre est :
3. La base est le cercle circonscrit au polygone.
Circonscrit dans un triangle quelconque :
Là-dedans :
- a, b, c sont les longueurs des trois côtés du triangle
- p est le demi-périmètre du triangle :
Circonférence d'un triangle rectangle : hypoténuse
Périphérie du triangle équilatéral : côté
Circonférence du carré : côté
Par exemple:
Calculer le rayon de la base du cylindre circonscrit à la pyramide régulière S.ABC dans les cas suivants :
un. ABC est un triangle rectangle en A avec AB = a et AC = a√3
b. ABC a AB= 5 ; CA= 7; BC=8
Prix:
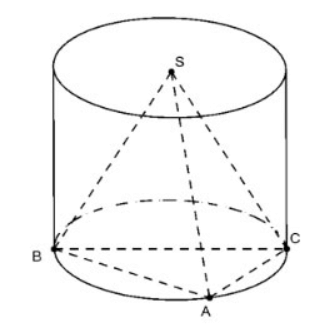
un. Hypoténuse
Parce que ABC est un angle droit en A, le rayon R=0,5.BC=a
b. Le demi-périmètre du triangle ABC est
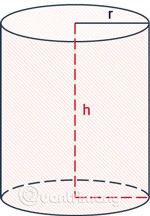
Qu'est-ce qu'un cylindre circulaire ?
Un cylindre circulaire est un cylindre avec deux bases circulaires égales et parallèles entre elles.
Les cylindres sont utilisés assez couramment dans les problèmes de géométrie, du plus simple au plus complexe, dans lesquels la formule de calcul de l'aire et du volume des cylindres est souvent utilisée différemment. Si vous savez déjà comment calculer l'aire et la circonférence d'un cercle, vous pouvez facilement déduire les formules de calcul du volume, de l'aire latérale et de l'aire totale d'un cylindre.
Formule de calcul de la section transversale d'un cylindre
Couper le cylindre par le plan (P) passant par l'axe
- La section transversale résultante est un rectangle.
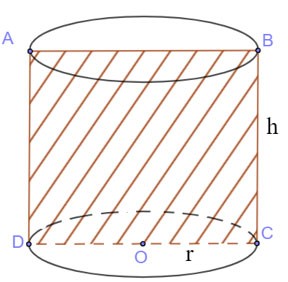 |
Section transversale :
SABCD = BC.CD = 2r.h
|
Couper le cylindre par un plan (P) parallèle et à une distance x de l'axe
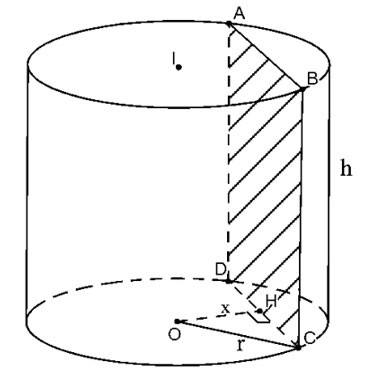 |
La section transversale résultante est le rectangle ABCD comme indiqué ci-dessus.
Soit H le milieu de CD, on a OH ⊥ CD=>
Par conséquent, la section transversale
|
Couper le cylindre par un plan (P) non perpendiculaire à l'axe mais couper toutes les génératrices du cylindre
 |
La section transversale formée est un cercle de centre O' et de rayon O'A'=r
Section transversale : S= πr2
|
Couper le cylindre par un plan (P) non perpendiculaire à l'axe mais couper toutes les génératrices du cylindre.
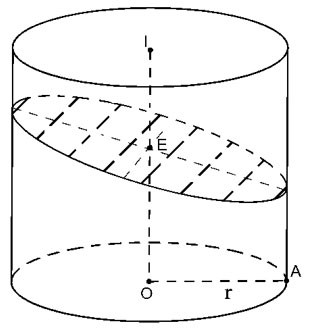 |
La section transversale résultante est une ellipse (E) avec un axe mineur 2r => a=r
Le grand axe est égal à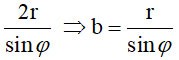
avec 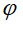 est l'angle entre l'axe OI et (P) est l'angle entre l'axe OI et (P)
Par conséquent, l'aire S = π. ab=
|
Exemple de calcul de l'aire d'un cylindre
Leçon 1 :
La zone latérale d'un cylindre a une circonférence de base circulaire de 13 cm et une hauteur de 3 cm.
Prix:
Nous avons : circonférence du cercle C = 2R.π = 13cm, h = 3cm
Donc l'aire latérale du cylindre est :
Sxq = 2πr.h = Ch = 13,3 = 39 (cm²)
Leçon 2 : Soit un cylindre avec un rayon de cercle de base de 6 cm, tandis que la hauteur de la base au sommet du cylindre est de 8 cm d'épaisseur. Quelle est l'aire latérale et l'aire totale du cylindre ?
Prix
Selon la formule, nous avons le demi-cercle de base r = 6 cm et la hauteur du cylindre h = 8 cm. Par conséquent, nous avons la formule pour calculer l'aire latérale d'un cylindre et l'aire totale d'un cylindre comme suit :
Surface du cylindre = 2 x π xrxh = 2 x π x 6 x 8 = ~ 301 cm²
Aire totale du cylindre = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm²
Leçon 3 : Un cylindre a un rayon de base de 7 cm et une aire latérale de 352 cm2.
Alors, la hauteur du cylindre est :
(A) 3,2 cm; (B) 4,6 cm; (C) 1,8 cm
(D) 2,1 cm; (E) Un autre résultat
Veuillez sélectionner le résultat correct.
Solution : Nous avons
Donc, la réponse E est correcte.
Leçon 4 : La hauteur d'un cylindre est égale au rayon du cercle de base. La surface latérale du cylindre est de 314 cm2. Calculez le rayon du cercle de base et le volume du cylindre (arrondissez le résultat à deux décimales).
Prix:
La surface latérale du cylindre est de 314 cm2
Nous avons Sxq = 2.π.rh = 314
Où r = h
Donc 2πr² = 314 => r² ≈ 50 => r ≈ 7,07 (cm)
Volume du cylindre : V = π.r2.h = π.r3 ≈ 1109,65 (cm³).
Nous espérons que l'article ci-dessus vous a aidé à saisir les connaissances de base et avancées sur les cylindres, comment calculer la surface totale et la surface latérale d'un cylindre.










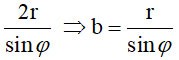
 est l'angle entre l'axe OI et (P)
est l'angle entre l'axe OI et (P)












