La formule de calcul de l'aire et du périmètre d'un parallélogramme est une connaissance de base. Veuillez vous référer à la formule que Quantrimang.com a compilée ci-dessous.
Table des matières
1. Aire du parallélogramme
L'aire d'un parallélogramme est mesurée par la taille de la surface, qui est la partie plane visible du parallélogramme.
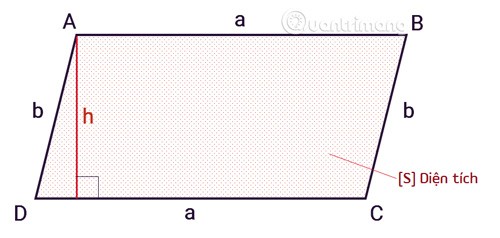
L'aire d'un parallélogramme est calculée par la formule égale au produit de la base par la hauteur.
SABCD = axh
Là-dedans :
Sest l'aire d'un parallélogramme.aest la base du parallélogramme.hest la hauteur, du sommet à la base, d'un parallélogramme.
2. Périmètre du parallélogramme
Le périmètre d'un parallélogramme est calculé en additionnant la longueur des lignes entourant la forme, qui est également la ligne entourant toute la zone, égale à 2 fois la somme de n'importe quelle paire de côtés adjacents.
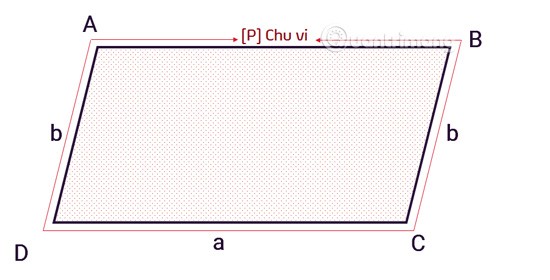
En d’autres termes, le périmètre d’un parallélogramme est la somme des longueurs des quatre côtés. La formule spécifique est la suivante :
C = 2 x (a+b)
Là-dedans :
Cest le périmètre d'un parallélogramme.aet bsont des côtés adjacents d'un parallélogramme.
3. Qu'est-ce qu'un parallélogramme ?
Définir
Un parallélogramme est un quadrilatère avec 2 paires de côtés parallèles ou 1 paire de côtés parallèles et égaux. Un parallélogramme a deux angles opposés égaux et deux diagonales qui se coupent au milieu de la forme.
Le parallélogramme peut être considéré comme un cas particulier de trapèze.
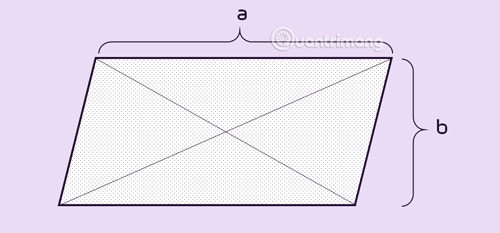
Propriétés du parallélogramme
En parallélogramme :
- Les côtés opposés sont égaux.
- Les angles opposés sont égaux.
- Deux diagonales se croisent au milieu de chaque ligne.
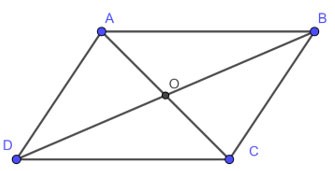
ABCD est un parallélogramme, AC coupe BD en O. Alors :
• AB = CD, AD = BC
•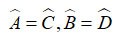
• OA = OC, OB = OD
Signes de reconnaissance
a) Un quadrilatère dont les côtés opposés sont parallèles est un parallélogramme.
b) Un quadrilatère dont les côtés opposés sont égaux est un parallélogramme.
c) Un quadrilatère avec deux côtés opposés parallèles et égaux est un parallélogramme.
d) Un quadrilatère dont les angles opposés sont égaux est un parallélogramme.
e) Un quadrilatère dont deux diagonales se coupent au milieu de chacune est un parallélogramme.
4. Questions à choix multiples pour réviser les parallélogrammes
Exercice 1 : Choisissez la mauvaise phrase.
A. Un parallélogramme a deux diagonales qui se coupent au milieu de chaque diagonale.
B. Le parallélogramme a deux angles opposés égaux
C. Un parallélogramme possède deux diagonales perpendiculaires l’une à l’autre.
D. Deux parallélogrammes ont deux paires de côtés opposés parallèles.
Solution
En parallélogramme :
+ Le parallélogramme a des côtés opposés parallèles
+ Les côtés opposés sont égaux
+ Deux diagonales se croisent au milieu de chaque ligne, donc C est incorrect.
La bonne réponse est : C
Exercice 2 : Étant donné le parallélogramme ABCD avec  = α > 900. À l'extérieur du parallélogramme, tracez les triangles équilatéraux ADE, ABF. Quel type de triangle est le triangle CEF ? Choisissez la meilleure réponse
A. Triangle
B. Triangle isocèle
C. Triangle équilatéral
D. Triangle obtus
Répondre:
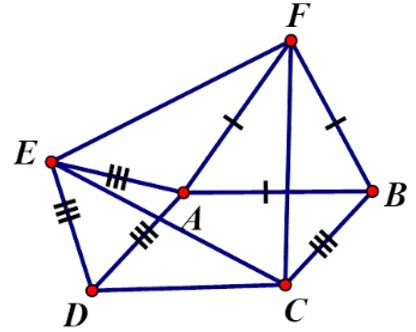

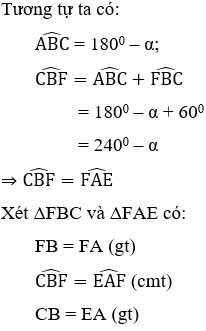
⇒ ΔFBC = ΔFAE (cgc) ⇒ CF = FE (2)
De (1) et (2) nous pouvons déduire que CF = FE = EC, donc le triangle CEF est équilatéral.
Leçon 3 : Choisissez la mauvaise phrase. ABCD est un parallélogramme. Alors:
A. AB = CD
B. AD = BC
C. Test du parallélogramme avec réponses
D. AC = BD
Solution
En parallélogramme :
+ Le parallélogramme a des côtés opposés parallèles
+ Les côtés opposés sont égaux
+ Deux diagonales se croisent au milieu de chaque ligne, donc D est incorrect.
Leçon 4 : Complétez le blanc avec la phrase appropriée : « Un quadrilatère avec deux diagonales… est un parallélogramme. »
A. égal
B. intersection
C. se croisent au milieu de chaque ligne
D. parallèle
Solution
Signes:
Un quadrilatère dont deux diagonales se coupent au milieu de chacune est un parallélogramme.
Leçon 5 : Choisissez la mauvaise phrase :
A. Un quadrilatère avec deux paires de côtés opposés parallèles est un parallélogramme.
B. Un trapèze avec deux angles égaux adjacents à une base est un parallélogramme.
C. Un quadrilatère avec deux paires de côtés opposés égaux est un parallélogramme.
D. Un quadrilatère avec deux paires d’angles opposés égaux est un parallélogramme.
Solution
Signes:
+ Un quadrilatère avec des côtés parallèles opposés est un parallélogramme donc A est correct.
+ Un quadrilatère dont les côtés opposés sont égaux est un parallélogramme, donc D est correct.
+ Un quadrilatère dont les angles opposés sont égaux est un parallélogramme, donc D est correct.
Sachant qu'un trapèze avec deux angles égaux adjacents à une base est un trapèze isocèle, B est donc incorrect.
La bonne réponse est : B
5. Exemples de calcul du périmètre et de l'aire d'un parallélogramme
Exemple 1 : Soit un parallélogramme avec une base de 12 cm, un côté de 7 cm et une hauteur de 5 cm. Calculer le périmètre et l'aire de ce parallélogramme ?
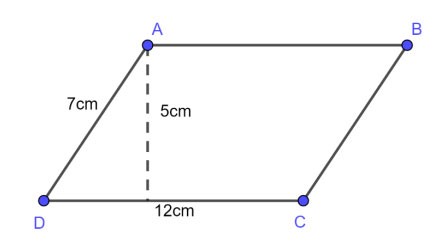
Prix:
Le périmètre du parallélogramme est :
P = 2 x (12 + 7) = 38 (cm)
L'aire d'un parallélogramme est :
S = axh = 12 x 5 = 60 (cm2)
Exemple 2 :
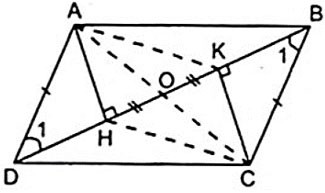
Étant donné le parallélogramme ABCD avec H, K étant les pieds des altitudes tirées des sommets A, C à BD, respectivement.
a) Démontrer que AHCK est un parallélogramme.
b) Soit O le milieu de HK. Démontrer que A, O, C sont colinéaires.
Instruire:
a) D'après l'hypothèse nous avons :
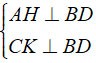 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 )
En appliquant les propriétés des côtés des parallélogrammes et les propriétés des angles alternes, nous avons :
 ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK
(cas hypoténuse – angle aigu)
⇒ AH = CK (les côtés correspondants sont égaux) ( 2 )
De (1) et (2) nous avons le quadrilatère AHCK avec des côtés opposés parallèles et égaux est un parallélogramme.
b) Appliquer les propriétés des diagonales du parallélogramme AHCK
Le parallélogramme AHCK possède deux diagonales AC et HK qui se croisent au milieu de chaque droite. Parce que O est le point médian de HK, O est également le point médian de AC.
⇒ A, O, C sont sur une ligne droite.
Outre les parallélogrammes, les formules de calcul de l'aire et du périmètre d'autres formes géométriques courantes telles que les losanges , les carrés , les trapèzes , les rectangles ... sont également très importantes et largement appliquées dans les études et la vie.
Nous espérons que grâce à l’article ci-dessus, vous avez mieux compris et saisi les connaissances de base sur les parallélogrammes. Veuillez laisser un commentaire ci-dessous si vous avez des questions ou des commentaires à discuter avec Quantrimang.com.




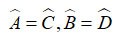



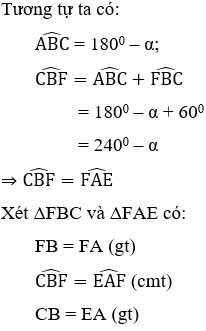


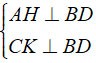 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 ) ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK











