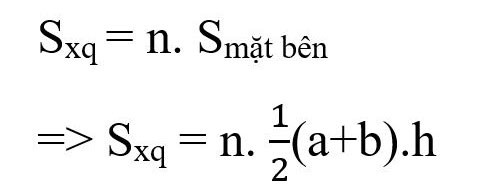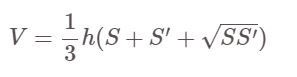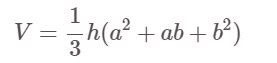Comment récupérer laccès au disque dur, corriger lerreur dimpossibilité douvrir le disque dur
Dans cet article, nous vous expliquerons comment récupérer l'accès à votre disque dur en cas de panne. Suivez-nous !
Formule de calcul du volume dune pyramide tronquée, de laire latérale et de laire totale dune pyramide tronquée
Apprenons ce qu'est une pyramide tronquée, comment calculer le volume d'une pyramide tronquée, l'aire latérale et l'aire totale d'une pyramide tronquée dans l'article ci-dessous.
Table des matières
- Définition de frustum
- Formule de calcul de l'aire d'une pyramide tronquée
- Formule de calcul du volume d'une pyramide tronquée
Définition de frustum
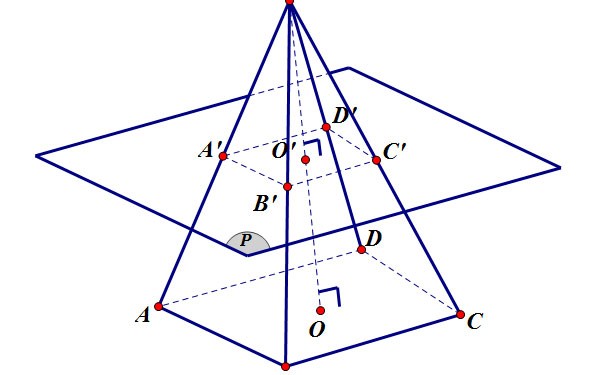
Une pyramide tronquée est une partie d'un polyèdre, située entre la base et la section transversale coupée par un plan parallèle à la base de la pyramide.
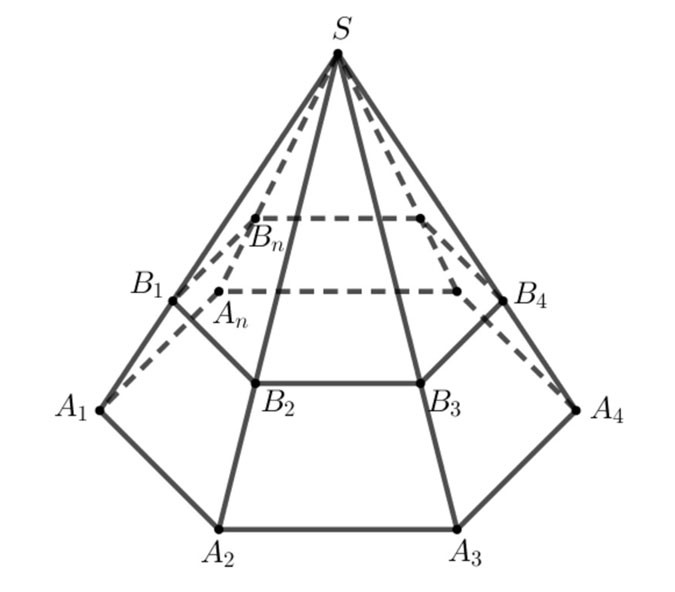
- La figure constituée des polygones A1A2...An,B1B2...BnA1A2...An,B1B2...Bn et des trapèzes A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn est appelée pyramide tronquée, notée A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn.
- En termes simples, une pyramide tronquée est formée à partir de la pyramide S.A1A2...AnS.A1A2...An après avoir coupé la pyramide S.B1B2...Bn.S.B1B2...Bn.
+ Les polygones A1A2...An,B1B2...BnA1A2...An,B1B2...Bn sont appelés les deux bases,
+ Les trapèzes A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn sont appelés faces latérales.
+ Les segments de droite A1B1,A2B2,...,AnBnA1B1,A2B2,...,AnBn sont appelés les bords latéraux, les bords de la surface de base sont appelés les bords de base.
+ La distance entre les deux bases est appelée la hauteur de la pyramide tronquée.
Propriétés de la pyramide tronquée :
- Les deux bases sont deux polygones (triangles, quadrilatères, pentagones, etc.) avec des côtés parallèles correspondants et des rapports égaux de côtés correspondants.
- Les faces latérales sont toutes des trapèzes.
- Les lignes contenant les bords latéraux convergeront vers un point (le sommet de la pyramide).
- Une pyramide tronquée est une pyramide dont les bases sont des polygones réguliers (à côtés égaux). Par conséquent, les faces latérales d'un tronc de cône sont toutes des trapèzes égaux.
Formule de calcul de l'aire d'une pyramide tronquée
Surface d'une pyramide tronquée
L'aire latérale d'une pyramide tronquée est l'aire des faces environnantes, la partie entourant la pyramide tronquée, à l'exclusion de l'aire des deux bases.
Comment calculer l'aire latérale d'une pyramide tronquée : Calculez l'aire de chaque face latérale (trapèzes) de la pyramide tronquée selon la formule de calcul de l'aire d'un trapèze normal , puis calculez l'aire totale.
Formule de calcul de l'aire d'une pyramide tronquée régulière :
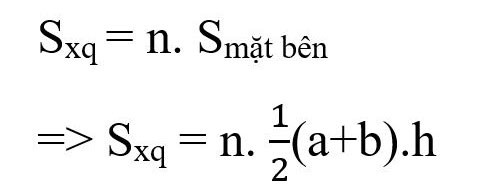
Là-dedans :
- Sxq : environs
- n : nombre de faces latérales de la pyramide tronquée (égal au nombre d'arêtes du polygone de base)
- a, b : longueurs des côtés des bases supérieure et inférieure respectivement
- h : hauteur des côtés des quadrilatères.
Exemple 1 :
Calculer l'aire latérale d'une pyramide tronquée quadrilatère régulière avec des arêtes de base de 10 cm et 15 cm et une hauteur de côté de 12 cm.
Prix:
La face latérale d'une pyramide tronquée quadrilatère régulière est un trapèze isocèle, donc l'aire d'une face latérale est :
Une pyramide tronquée quadrilatère régulière a 4 côtés égaux, donc son aire latérale est :
150 x 4 = 600 (cm2)
Exemple 2 : Calculer l'aire latérale d'une pyramide tronquée quadrilatère régulière avec des arêtes de base de 6 cm et 8 cm et une hauteur de côté de 5 cm. Calculer l'aire latérale d'une pyramide tronquée quadrilatère régulière dont les arêtes de base sont de 6 cm et 8 cm.
Prix:
La face latérale d'une pyramide tronquée quadrilatère régulière est un trapèze isocèle, donc l'aire d'une face latérale est égale à
Une pyramide tronquée quadrilatère régulière a quatre côtés égaux, donc son aire latérale est égale à
35 x 4 = 140 (cm2)
Surface totale d'une pyramide tronquée
L'aire totale d'une pyramide tronquée est égale à la somme de l'aire latérale et de l'aire des deux bases.
Formule : Stp = Sxq + Grand fond + Petit fond
Là-dedans :
- Stp : Superficie totale
- Sxq : Environs
- Grande base : Grande surface de base
- Petite base : Petite surface de base
Par exemple:
Calculez l'aire totale d'une pyramide tronquée régulière selon les dimensions données sur la figure.
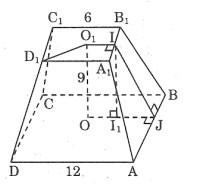
Prix:
Nous avons:
AD = 12 ⇒ OJ = 6
Dessinez II1 ⊥ OJ nous avons : I1J = 3
En appliquant le théorème de Pythagore au triangle rectangle II1J, nous avons :
IJ2 = II12 + I1J2 = 92 + 32 = 90
Ainsi:
L'aire d'un côté d'un trapèze est :
La superficie environnante est égale à :
L'aire de la base supérieure est : S = 6 x 6 = 36 (unités)
L'aire de la base inférieure est : S = 12 x 12 = 144 (unités)
L'aire totale d'une pyramide tronquée est égale à :
Formule de calcul du volume d'une pyramide tronquée
Recette:
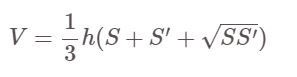
Là-dedans :
- V : volume de la pyramide tronquée
- S, S' sont respectivement les aires des grandes et petites bases de la pyramide.
- h : hauteur de la pyramide, c'est-à-dire la distance entre les deux grandes et petites bases
Une pyramide tronquée est-elle un carré (quadrilatère régulier) :
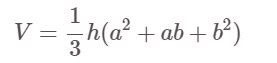
Là-dedans :
- V : Volume
- h : Hauteur de la pyramide
- a, b sont les longueurs des bords de la grande base et de la petite base respectivement.
Comment utiliser Conversation Awareness et Live Listen sur les AirPods
À première vue, les AirPods ressemblent à n'importe quel autre écouteur sans fil. Mais tout a changé avec la découverte de quelques fonctionnalités peu connues.
Tout sur iOS 26
Apple a présenté iOS 26 – une mise à jour majeure avec un tout nouveau design en verre dépoli, des expériences plus intelligentes et des améliorations des applications familières.
Healthy snacks that help you lose weight
Craving for snacks but afraid of gaining weight? Dont worry, lets explore together many types of weight loss snacks that are high in fiber, low in calories without making you try to starve yourself.
Do you really need rest days between workouts?
Rest and recovery are not the same thing. Do you really need rest days when you schedule a workout? Lets find out!
Les meilleurs ordinateurs portables pour étudiants en 2025
Les étudiants ont besoin d'un ordinateur portable spécifique pour leurs études. Il doit être non seulement suffisamment puissant pour être performant dans la filière choisie, mais aussi suffisamment compact et léger pour être transporté toute la journée.
Comment ajouter une imprimante à Windows 10
L'ajout d'une imprimante à Windows 10 est simple, bien que le processus pour les appareils filaires soit différent de celui pour les appareils sans fil.
Comment vérifier la RAM et vérifier les erreurs de RAM sur votre ordinateur avec le taux de précision le plus élevé
Comme vous le savez, la RAM est un composant matériel essentiel d'un ordinateur. Elle sert de mémoire pour le traitement des données et détermine la vitesse d'un ordinateur portable ou de bureau. Dans l'article ci-dessous, WebTech360 vous présente quelques méthodes pour détecter les erreurs de RAM à l'aide d'un logiciel sous Windows.
Why doesnt the freezer have a light but the refrigerator does?
Refrigerators are familiar appliances in families. Refrigerators usually have 2 compartments, the cool compartment is spacious and has a light that automatically turns on every time the user opens it, while the freezer compartment is narrow and has no light.
2 Ways to Fix Network Congestion That Slows Down Wi-Fi
Wi-Fi networks are affected by many factors beyond routers, bandwidth, and interference, but there are some smart ways to boost your network.
Comment rétrograder diOS 17 à iOS 16 sans perte de données avec Tenorshare Reiboot
Si vous souhaitez revenir à la version stable d'iOS 16 sur votre téléphone, voici le guide de base pour désinstaller iOS 17 et rétrograder d'iOS 17 à 16.
Que se passe-t-il dans le corps lorsque vous mangez du yaourt tous les jours ?
Le yaourt est un aliment merveilleux. Est-il bon de manger du yaourt tous les jours ? Si vous mangez du yaourt tous les jours, comment votre corps va-t-il changer ? Découvrons-le ensemble !
Quel type de riz est le meilleur pour la santé ?
Cet article présente les types de riz les plus nutritifs et comment maximiser les bienfaits pour la santé du riz que vous choisissez.
Comment se réveiller à lheure le matin
Établir un horaire de sommeil et une routine de coucher, changer votre réveil et ajuster votre alimentation sont quelques-unes des mesures qui peuvent vous aider à mieux dormir et à vous réveiller à l’heure le matin.
Latest Bathroom Tower Defense Codes and How to Enter Codes
Get Bathroom Tower Defense Roblox game codes and redeem them for exciting rewards. They will help you upgrade or unlock towers with higher damage.