Formule de calcul de la surface et du volume dune sphère

Apprenons et révisons la formule de calcul de la surface et du volume d'une sphère avec Quantrimang.com dans l'article ci-dessous.

Table des matières

• Qu'est-ce qu'une sphère ?
  • Qu'est-ce qu'une sphère ?
• Formule de calcul de la surface et du volume d'une sphère
  • Formule de calcul de la surface d'une sphère
  • Formule pour calculer le volume d'une sphère :
• Formule de calcul du rayon d'une sphère
  • La sphère circonscrite à la pyramide a un côté perpendiculaire à la base.
  • Tétraèdre carré (c'est un cas particulier de la formule 1)
  • Un prisme vertical a une base qui est un polygone inscrit.
  • Formule d'un tétraèdre dont les sommets sont les sommets d'un prisme droit
  • Formule de calcul du rayon d'une sphère pour une pyramide dont les faces latérales sont perpendiculaires à la base
• Exemples de calcul de la surface et du volume d'une sphère

Qu'est-ce qu'une sphère ?

Une sphère est le lieu de points équidistants d'un point fixe O donné rdans l'espace à 3 dimensions. Le point O est appelé le centre et la distance rest appelée le rayon de la sphère.

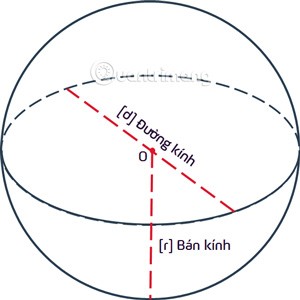
Qu'est-ce qu'une sphère ?

Une sphère est un ensemble de points situés à l'intérieur d'une sphère et une sphère est appelée sphère ou sphère de centre O et de rayon r = OA.

Formule de calcul de la surface et du volume d'une sphère

Formule de calcul de la surface d'une sphère

L'aire de surface d'une sphère est quatre fois l'aire d'un grand cercle, qui est quatre fois la constante Pi multipliée par le carré du rayon de la sphère.

Formule pour calculer le volume d'une sphère :

Le volume d'une sphère, également appelé volume d'une sphère, est calculé en multipliant les trois quarts de Pi par le cube du rayon de la sphère.

Là-dedans :

• Sest l'aire de la surface de la sphère
• Vest le volume d'une sphère
• rest le rayon de la sphère/sphère
• dest une sphère/sphère

Formule de calcul du rayon d'une sphère

La sphère circonscrite à la pyramide a un côté perpendiculaire à la base.

• Rd est le rayon de la base.
• h est la longueur du côté perpendiculaire à la base.

Par exemple : Soit une pyramide S.ABCD à base rectangulaire avec AB = 3a, BC = 4a, SA = 12a et SA perpendiculaire à la base. Calculer le rayon R de la sphère circonscrite à la pyramide S.ABCD.

Solution : Nous avons

Donc

Tétraèdre carré (c'est un cas particulier de la formule 1)

Le bloc carré OABC a OA, OB, OC, perpendiculaires entre eux et a :

Par exemple:

Le tétraèdre OABC a OA, OB, OC, mutuellement perpendiculaires et a un rayon de sphère circonscrite de . Le plus grand volume du tétraèdre OABC

Solution : Nous avons

D'autre part, nous avons :

Selon l'inégalité AM - GM, nous avons :

Un prisme vertical a une base qui est un polygone inscrit.

Là-dedans :

• Rd est le rayon de la base
• h est la longueur du côté.

Exemple 1 : Étant donnée une sphère de rayon R circonscrite à un cube de côté a. Laquelle des affirmations suivantes est vraie ?

UN.

B.

C.

D.

Solution : Nous avons

Donc, la réponse est C.

Formule d'un tétraèdre dont les sommets sont les sommets d'un prisme droit

Le tétraèdre (H1) a des sommets qui sont les sommets du prisme vertical (H2), alors :

Formule de calcul du rayon d'une sphère pour une pyramide dont les faces latérales sont perpendiculaires à la base

Dans laquelle R, d est le rayon de la base ; a, x sont respectivement la longueur de l'intersection de la face latérale et de la base, l'angle au sommet de la face latérale regardant vers le bas vers la base.

Ou vous pouvez utiliser la formule

Dans laquelle : Rb est le rayon circonscrit de la face latérale et a est la longueur de l'intersection de la face latérale et de la base.

Par exemple: 

Étant donné la pyramide S.ABCD à base carrée, le triangle équilatéral SAD de côté √2a et situé dans un plan perpendiculaire à la base. Calculer le rayon R de la sphère circonscrite à la pyramide S.ABCD.

UN.

B.

Solution : Nous avons

Donc la bonne réponse est B.

Exemples de calcul de la surface et du volume d'une sphère

Leçon 1 : Soit un cercle dont la circonférence est de 31,4 cm. Calculez le volume d'une sphère de rayon égal au rayon du cercle donné.

Prix:

Circonférence du cercle C = 2πr = 31,4 cm

=> Rayon r = C/2π = 5 cm

Le volume de la sphère donnée est :

V = ⁴⁄₃πr³ = 4/3.3.14.(5)³ = 523,3 cm³

Leçon 2 : Calculer le volume d'une sphère de diamètre d = 4 cm.

Prix:

Rayon r = d/2 = 2 cm

Le volume de la sphère est :

V = ⁴⁄₃πr³ = 4/3.3.14.(2)³ = 33,49 cm³

Leçon 3 :

Laissez un cercle de diamètre 4a tourner autour de son diamètre. Quel est alors le volume du solide en rotation ?

Solution : Étant donné un cercle de diamètre 4a tournant autour de son diamètre, nous obtenons une sphère de diamètre 4a ou de rayon R = 2a.

Le volume de la sphère est :

Leçon 4 :

La sphère de rayon R√3 a une aire de :

A. 4√3πR2

B. 4πR2

C. 6πR2

D. 12πR2

Solution : Appliquer la formule : S = 4πR2

L'aire de surface d'une sphère de rayon R√3 est : S = 4π(R√3)2 = 12πR2

Donc la réponse est D.

Deux formules courtes mais à retenir longtemps c'est assez difficile. Ajoutez l’article à vos favoris et ouvrez-le quand vous en avez besoin. J'espère que cet article vous sera utile.

En plus de la formule de calcul de l'aire de surface et du volume d'une sphère ci-dessus, vous pouvez également vous référer à la formule de calcul de l'aire de certaines autres formes de base telles que les triangles , les rectangles et les parallélogrammes. ..