Formule de calcul de la diagonale dun losange

Un losange est un quadrilatère à quatre côtés égaux, un quadrilatère à deux diagonales perpendiculaires entre elles au milieu de chaque droite est un losange, un parallélogramme à deux côtés adjacents égaux... Outre les carrés, les rectangles, les triangles... le losange est l'une des formes importantes en mathématiques et dans la vie.

Outre la formule de calcul du périmètre et de l'aire d'un losange , la manière de calculer la diagonale d'un losange - la ligne reliant les sommets opposés du losange entre eux - est également très importante.

L'article ci-dessous vous aidera à apprendre à calculer la diagonale d'un losange avec des exemples spécifiques, veuillez vous y référer.

Table des matières

• Diagonale d'un losange
• Propriétés des diagonales d'un losange
• Formule de calcul de la diagonale d'un losange
• Problème de calcul de la diagonale du losange

Diagonale d'un losange

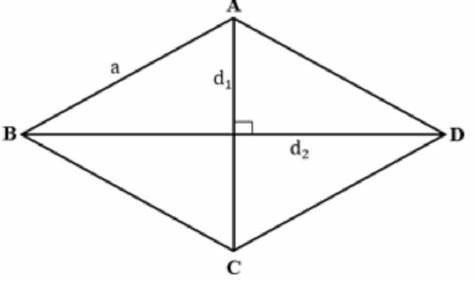
• La diagonale d'un losange est la ligne reliant deux sommets opposés du losange.
• Un losange a deux diagonales, et elles se coupent au milieu du losange.
• La diagonale divise le losange en deux triangles équilatéraux de côtés égaux.

Propriétés des diagonales d'un losange

Les deux diagonales d'un losange ont les propriétés suivantes :

• Deux diagonales égales : Les deux diagonales d'un losange sont de longueur égale.
• L'angle entre deux diagonales est un angle droit : Les deux diagonales d'un losange se coupent au milieu du losange et forment un angle droit.
• Les diagonales sont les axes de symétrie d'un losange : Chaque diagonale d'un losange est un axe de symétrie du losange, divisant le losange en deux moitiés symétriques.
• Les diagonales sont les diagonales de deux triangles équilatéraux : Chaque diagonale d'un losange est une diagonale de deux triangles équilatéraux, formés par des côtés égaux.
• Le produit des longueurs des deux diagonales est égal au produit des longueurs des deux côtés d'un losange : Le produit des longueurs des deux diagonales est égal au produit des longueurs des deux côtés d'un losange. Autrement dit, si nous désignons la diagonale par d et les côtés par a et b, nous avons d² = a² + b².

Ces propriétés sont des propriétés caractéristiques des losanges et sont utilisées dans de nombreux problèmes géométriques impliquant des losanges.

Formule de calcul de la diagonale d'un losange

Veuillez considérer l’exemple ci-dessous pour dériver la formule de calcul de la diagonale d’un losange.

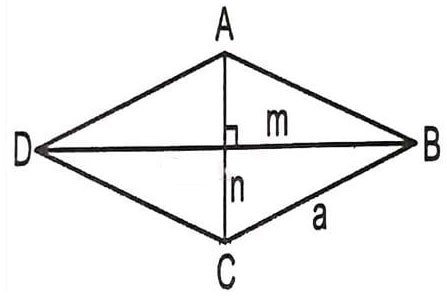
Supposons que nous devions calculer la longueur de la diagonale d'un losange ABCD avec le côté a et un angle ABC = 60 degrés -> quelle est la formule pour calculer la diagonale d'un losange dans ce cas ?

Solution:

Parce que ABCD est un losange, tous les côtés sont égaux à a.

Considérons le triangle ABC avec : AB = BC = a

Encore une fois : ABC = 60 degrés => Le triangle ABC est un triangle équilatéral de côté a.

=> AB = AC = BC = a

=> La longueur de la diagonale du losange est AC = BD = a.

La solution ci-dessus est l’une des formules les plus simples et les plus faciles à comprendre pour calculer la diagonale d’un losange.

Formule de calcul de la diagonale d'un losange en connaissant l'aire et la diagonale restante

D'après la formule de calcul de l'aire d'un losange :

S = (axb) : 2

Nous avons la formule pour la longueur de la diagonale comme suit :

a = S x 2 : b

ou

b = S x 2 : a

Là-dedans :

• S est la zone
• a et b sont les longueurs des deux diagonales

Utilisez les propriétés géométriques d'un losange pour calculer la longueur de la diagonale sans utiliser le théorème de Pythagore. Spécifiquement:

La diagonale d'un losange est la moyenne des deux hauteurs.

Diagonale = racine carrée de (hauteur longue + hauteur courte)²

La diagonale d'un losange est la moitié du périmètre du losange.

Diagonale = 1/2 x périmètre du losange.

Problème de calcul de la diagonale du losange

Problème 1 : Soit un losange d'une aire de 360 ​​centimètres carrés et d'une diagonale de 24 centimètres. Calculer la longueur de la deuxième diagonale

Solution:

Selon la formule de l'aire d'un losange : axb : 2

Nous avons la deuxième diagonale : 360 x 2 : 24 = 30 cm

Réponse : 30 cm

Problème 2 :

Un losange a une aire de 4dm, la longueur d'une diagonale est de 3/5 dm. Calculez la longueur de la deuxième diagonale. Solution:

La longueur de la deuxième diagonale est :

(4 x 2) : 3/5 = 40/3 (dm)

Leçon 3 : Les deux diagonales d’un losange ont des longueurs de 160 cm et 120 cm. Calculez la hauteur du losange, sachant que le rapport entre la hauteur et la longueur du côté du losange est de 24:25.

Solution:

L'aire du losange est : 160.120:2 = 9 600 (cm2).

Étant donné que le rapport entre la hauteur et la longueur du côté d'un losange est de 24:25, nous pouvons considérer que la hauteur du losange est de 24a et le côté du losange est de 25a.

On a alors l'aire du losange : 25a.24a = 9 600 a2 = 16 a = 4 cm.

La hauteur du losange est : 24,4 = 96 (cm).

Donc la hauteur du losange est de 96 cm.

Leçon 4 : 

Étant donné le losange ABCD avec une longueur de côté de 12,5 cm, une hauteur de 6,72 cm et AC est plus petit que BD. Quelles sont les longueurs des diagonales AC et BD respectivement ?

Prix:

Appliquez la formule pour calculer l'aire d'un losange : S = ha = 6,72 x 12,5 = 84cm.
=> 1/2 AC x BD = 84 => 2AC.BD = 336

Soit O l'intersection des deux diagonales d'un losange.

Nous avons AOB est un triangle rectangle en O donc AB2 = OA2 + OB2

Dans lequel, OA = 1/2 AC, OB = 1/2 BD

=> 12,52 = 1/4 (AC2 + BD2) <=> 625 = AC2 + BD2

AC2 + BD2 = 625 <=> AC2 + BD2+ 2AC.BD = 625 + 336 <=> (AC + BD)2 = 961 <=> AC + BD = 31 (1)

AC2 + BD2 = 625 <=> AC2 + BD2- AC.BD = 625 -336 <=> (BD - AC)2 = 289 <=> BD - AC = 17 (D'après le problème BD > AC) (2)

De (1) et (2), nous avons :

BD = 24, CA = 7 cm.

Leçon 5 : 

Le losange ABCD a des côtés égaux à 10 unités. Calculer la longueur de la diagonale du losange.

Solution : La longueur de la diagonale du losange ABCD est :

Diagonale = racine carrée de 2(10²) = racine carrée de 200 = 14,14 unités de longueur.

Ainsi, la longueur de la diagonale du losange ABCD est de 14,14 unités de longueur.

Leçon 6 :

Le losange ABCD a une diagonale de 12 unités. Calculer le périmètre du losange.

Solution : Puisqu'un losange a quatre côtés égaux, son périmètre sera la somme des longueurs des quatre côtés, c'est-à-dire :

Périmètre = 4 x longueur du côté = 4 x 6 = 24 unités de longueur.

Ainsi, le périmètre du losange ABCD est de 24 unités de longueur.