Quest-ce quun nombre rationnel ? Quest-ce quun nombre irrationnel ?

Les définitions et les formules des nombres rationnels et irrationnels sont des connaissances importantes en mathématiques que les élèves doivent comprendre pour avoir une base mathématique solide. L'article suivant vous présente la définition, les propriétés et les formes mathématiques des nombres rationnels et irrationnels. Veuillez vous y référer.

Nombres rationnels, nombres irrationnels

• Qu'est-ce qu'un nombre rationnel ?
  • Classification des nombres rationnels
  • Représenter des nombres rationnels sur une droite numérique
  • Additionner et soustraire des nombres rationnels
  • Multiplier et diviser des nombres rationnels
  • Valeur absolue d'un nombre rationnel
  • Comparer deux nombres rationnels
  • Formule pour calculer la puissance d'un nombre rationnel
• Qu'est-ce qu'un nombre irrationnel ?
  • Concept des nombres irrationnels
  • Propriétés des nombres irrationnels
• Quelle est la différence entre les nombres rationnels et irrationnels ?
• Relation entre les ensembles de nombres
• Exercices sur les nombres rationnels

Qu'est-ce qu'un nombre rationnel ?

- Les nombres rationnels sont l'ensemble des nombres qui peuvent être écrits sous forme de fractions (quotients). Autrement dit, un nombre rationnel peut être représenté par un nombre décimal récurrent infini.

- Les nombres rationnels s'écrivent comme , où a et b sont des entiers mais b doit être différent de 0.

- est l'ensemble des nombres rationnels.

=> Ensemble de nombres rationnels : .

Par exemple : , , … sont des nombres rationnels.

• Tout entier a est un nombre rationnel car l'entier a peut être écrit sous la forme .

Par exemple : nous avons des nombres rationnels.

Nous avons:

Commentaire : ce sont tous des nombres rationnels.

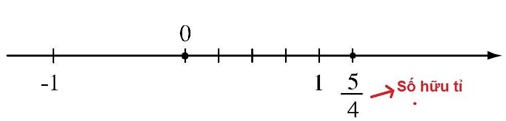
Classification des nombres rationnels

Les nombres rationnels sont divisés en deux types : les nombres rationnels négatifs et les nombres rationnels positifs. Spécifiquement:

• Nombres rationnels négatifs : inclure les nombres rationnels inférieurs à 0.
• Nombres rationnels positifs : inclure les nombres rationnels supérieurs à 0.

Remarque : le nombre 0 n’est ni un nombre rationnel négatif ni un nombre rationnel positif.

Nature

• L'ensemble des nombres rationnels est un ensemble dénombrable.
• Propriété commutative :
• Propriété d'addition avec 0 :
• Propriétés combinées :

Représenter des nombres rationnels sur une droite numérique

- Pour représenter les nombres rationnels sur la droite numérique, nous suivons ces facteurs :

Étape 1 : Écrivez le nombre rationnel sous forme de fraction

Étape 2 : Divisez le segment de ligne unitaire en b parties égales pour obtenir un nouveau segment unitaire qui est l'ancienne unité.

Étape 3 : Le nombre rationnel est représenté par le point A étant une distance d'une nouvelle unité du point 0.

• A est à gauche de 0 s'il s'agit d'un nombre négatif.
• A est à droite de 0 s'il s'agit d'un nombre positif.

Par exemple : Dans la figure, le point P représente le nombre rationnel :

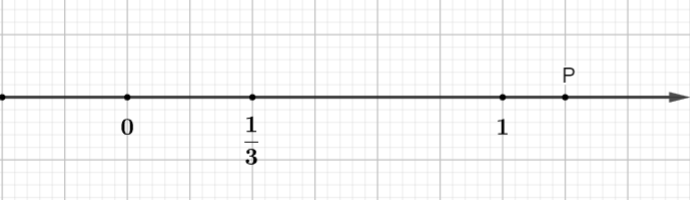
Instruire

Le segment de ligne unitaire est divisé en 6 parties égales (la nouvelle unité est 1/6 de l'ancienne unité)

Le point P est situé à une distance de 7 nouvelles unités du point O.

Et le point P est à droite du point O donc P est un nombre rationnel positif.

Donc P représente un nombre rationnel.

Additionner et soustraire des nombres rationnels

i) Règles d'addition et de soustraction de deux nombres rationnels

Nous pouvons additionner et soustraire deux nombres rationnels x et y en les écrivant sous forme de deux fractions, puis en appliquant les règles d’addition et de soustraction de fractions.

Chez nous nous avons :

ii) Propriétés

- L'addition des nombres rationnels a les propriétés de l'addition des fractions : Commutative, associative, addition avec 0, addition avec les contraires.

- Nous avons:

a) Propriété commutative :

b) Propriétés associatives :

c) Ajouter 0 :

d) Ajoutez le nombre opposé :

iii, Règles de transition

Lorsque nous déplaçons un terme d’un côté à l’autre d’une équation, nous devons changer le signe de ce terme.

Dans Q, nous avons une somme algébrique, dans laquelle nous pouvons échanger des termes, mettre des parenthèses pour regrouper des termes arbitrairement comme des sommes algébriques dans l'ensemble des entiers.

• Avec si alors
• Chez nous nous avons :

Multiplier et diviser des nombres rationnels

i) Règles de multiplication et de division de deux nombres rationnels

- Nous pouvons multiplier et diviser deux nombres rationnels en les écrivant sous forme de fractions, puis en appliquant les règles de multiplication et de division des fractions.

• Chez nous nous avons :
• Chez nous nous avons :

Par exemple:

Multiplier les nombres rationnels : 

Diviser les nombres rationnels : 

ii) Propriétés

- La multiplication des nombres rationnels possède également les mêmes propriétés que la multiplication des fractions : commutative, associative, multiplication par 1 et propriété distributive de la multiplication sur l'addition.

- Tout nombre rationnel non nul a un inverse.

- Nous avons:

• Propriété commutative : .
• Propriétés associatives : .
• Propriété de la multiplication par 1 : .
• Propriétés distributives : .
• Avec . L'inverse de a est .

Valeur absolue d'un nombre rationnel

- La valeur absolue d'un nombre rationnel a, noté , est la distance du point a au point 0 sur la droite numérique.

Par exemple:

(Parce que )

(Parce que )

Comparer deux nombres rationnels

- Avec 2 nombres rationnels, nous avons toujours soit ou soit .

- Pour comparer deux nombres rationnels, nous procédons comme suit :

• Écrivez sous forme de 2 fractions avec le même dénominateur positif :
• Comparez les numérateurs en tant qu'entiers a, b :

Par exemple : Comparez deux nombres rationnels : et

Nous avons:

Parce que c'est bon.

Formule pour calculer la puissance d'un nombre rationnel

Formules de calcul des puissances des nombres rationnels dont vous devez vous souvenir

• Produit de deux puissances de même base :
• Pouvoir du pouvoir
• La puissance d'un produit
• Puissance d'un quotient

Qu'est-ce qu'un nombre irrationnel ?

Concept des nombres irrationnels

• Lorsqu’on parle de nombres rationnels, on ne peut s’empêcher de mentionner les nombres irrationnels. Ce sont des nombres écrits sous forme de décimales infinies et non répétitives, notés .
• Les nombres réels qui ne sont pas des nombres rationnels ne peuvent pas être représentés sous forme de rapports.

Par exemple : 3,145248… est un nombre irrationnel.

Propriétés des nombres irrationnels

L'ensemble des nombres irrationnels est un ensemble indénombrable.

Par exemple:

Nombres irrationnels : 0,1010010001000010000010000001… (il s'agit d'un nombre décimal infini non répétitif)

Nombre de racines carrées : √2 (racine carrée)

Pi (π) : 3,14159 26535 89793 23846 26433 83279 50 288…..

Quelle est la différence entre les nombres rationnels et irrationnels ?

• Les nombres rationnels incluent des décimales récurrentes non terminales, tandis que les nombres irrationnels sont des décimales non répétitives non terminales.
• Les nombres rationnels ne sont que des fractions, tandis que les nombres irrationnels ont de nombreux types de nombres différents.
• Les nombres rationnels sont des nombres dénombrables, tandis que les nombres irrationnels sont des nombres indénombrables.

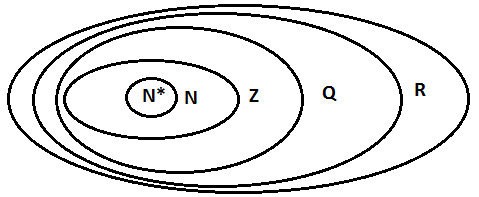
Relation entre les ensembles de nombres

Symboles des ensembles de nombres :

• N : Ensemble des nombres naturels
• N* : Ensemble de nombres naturels autres que 0
• Z : Ensemble d'entiers
• Q : L'ensemble des nombres rationnels
• I : Ensemble des nombres irrationnels

Nous avons : R = Q ∪ I.

Ensemble N; Z ; Q; R.

Alors la relation d'inclusion entre les ensembles de nombres est : N ⊂ Z ⊂ Q ⊂ R

Exercices sur les nombres rationnels

Forme 1 : Effectuer des calculs impliquant des nombres rationnels

Méthode de résolution : Pour résoudre les exercices sur la réalisation de calculs liés aux nombres rationnels, convertissez d'abord les nombres rationnels en fractions, puis appliquez les règles de calcul avec l'addition, la soustraction, la multiplication et la division des nombres rationnels.

Exemple : Calculer  

Répondre:

Forme 2 : Représentation des nombres rationnels sur la droite numérique

Solution : Vous devez déterminer si le nombre rationnel est un nombre rationnel positif ou un nombre rationnel négatif, puis passer aux étapes suivantes :

• Si le nombre rationnel a/b est un nombre rationnel positif : Sur la droite numérique, dans le sens positif, divisez la longueur de 1 unité en b parties égales. Prenez ensuite un point sur la direction positive de l'axe Ox, pointez une partie et déterminez la position du nombre rationnel a/b.
• Si le nombre rationnel a/b est un nombre rationnel négatif : Sur la droite numérique, dans le sens négatif de l'axe, divisez la longueur de 1 unité en b parties égales. Prenez ensuite un point sur la direction négative de l'axe Ox, pointez une partie et déterminez la position du nombre rationnel a/b.

Forme 3 : Comparaison de nombres rationnels

Solution : Convertissez les nombres rationnels donnés en fractions avec le même dénominateur positif, puis comparez les numérateurs. Plus avancé, nous pouvons comparer avec des fractions intermédiaires pour trouver la réponse.

Formulaire 4 : Déterminer si un nombre rationnel est négatif, positif ou 0

Méthode de résolution : Pour résoudre les exercices de type 4, les élèves doivent se baser sur les propriétés des nombres rationnels pour déterminer si le nombre rationnel est négatif, positif ou 0.

Par exemple : Étant donné le nombre rationnel x = (a – 25)/29, déterminez la valeur de a de telle sorte que :

• x est négatif
• x est positif
• x = 0

Répondre:

x est un nombre négatif => (a – 25)/29 < 0=""> a – 25 < 0=""> a <>

x est un nombre positif => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

x = 0 => (a – 25)/29 =0 0 => a – 25 = 0 => a = 25

Forme 5 : Trouver des nombres rationnels dans l'intervalle selon des conditions données

Solution : Si la question nécessite de trouver des nombres rationnels dans un intervalle selon des conditions données, nous devons placer les nombres rationnels dans le même numérateur ou dénominateur pour trouver la réponse.

Exemple : trouver la valeur de m pour supérieur à et inférieur à

Guide de réponses

Convertissez les fractions en dénominateurs communs comme suit :

Dénominateur commun : 18

D'après la question nous avons :

Formulaire 6 : Trouver x avec des nombres rationnels

Méthode pour résoudre les problèmes mathématiques : Pour les problèmes mathématiques permettant de trouver x avec des nombres rationnels, il est nécessaire d'effectuer une réduction du dénominateur commun et de convertir x en un côté et les termes restants en 1. À partir de là, calculez la valeur de x

Par exemple : Trouver x sachant x . (2/ 3) + 5/ 6 = 1/ 8

Répondre:

x . (2/ 3) + 5/ 6 = 1/ 8

=> x . (2/ 3) = 1/ 8 + 5/ 6

=> x = 46/ 48 : 2/ 3

=> x = 23 . 3 / 24 . 2

=> 23/16

Formulaire 7 : Trouver un tel que l'expression soit un entier

Méthode pour résoudre les problèmes mathématiques : Pour le problème de recherche de a, si le numérateur ne contient pas a, nous devons utiliser le signe de divisibilité. Si le numérateur contient un, utilisez le signe de divisibilité ou séparez le numérateur par le dénominateur. Si le problème nécessite de trouver a et b en même temps, regroupez a ou b et convertissez-les sous forme fractionnaire pour le calcul.

Exemple : Trouver l’entier a avec la condition que 8/(a – 1) soit un entier

Répondre:

Condition : a – 1 ≠ 0 => a ≠ 1

Soit a un entier => 8 est divisible par (a – 1)

=> (a – 1) est un facteur de 8 => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (a – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> a = {-7, -3, -1, 0, 3, 5, 9}

Nous espérons que l'article ci-dessus vous a aidé à comprendre ce que sont les nombres rationnels, ce que sont les nombres irrationnels, les types de nombres rationnels, ce que sont les symboles des nombres rationnels et comment reconnaître les nombres rationnels pour résoudre facilement les problèmes.

En plus des connaissances sur les nombres irrationnels et les nombres rationnels ci-dessus, vous pouvez vous référer à d'autres connaissances mathématiques telles que les fractions , les nombres mixtes , les décimales ...