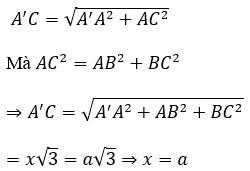Un prisme est un polygone avec deux bases parallèles et égales et des faces latérales en forme de parallélogramme.
Commentaire:
- Les faces latérales d'un prisme sont égales et parallèles entre elles.
- Les faces latérales sont des parallélogrammes.
- Les deux bases d'un prisme sont deux polygones égaux.
Quelle est la formule pour calculer le volume d'un prisme (prisme en V) et quelle est la formule pour calculer le volume d'un prisme vertical ? Veuillez vous référer à l'article ci-dessous.
Table des matières
1. Volume d'un prisme vertical
Formule de calcul du volume d'un prisme vertical :
Le volume d'un prisme droit est égal au produit de l'aire de la base multipliée par la hauteur.
Là-dedans
Vest le volume du prisme (unité m3)Best la surface de base (unité m2)hest la hauteur du prisme (unité m)
3. Classification des prismes
Prisme régulier
C'est un prisme vertical avec une base polygonale régulière. Les faces latérales du prisme sont toutes des rectangles égaux. Par exemple : prisme triangulaire régulier, quadrilatère régulier... alors on le comprend comme un prisme régulier.
Une base quadrilatérale régulière est appelée prisme quadrilatéral régulier.
Prisme triangulaire
- Un prisme triangulaire a 5 faces, 9 arêtes et 6 sommets.
- Les deux bases sont toutes deux triangulaires et parallèles l'une à l'autre ; Chaque face latérale est un rectangle ;
- Les côtés sont égaux ;
- La hauteur d'un prisme triangulaire est la longueur d'un côté.
Par exemple:
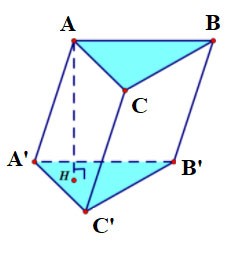
Le prisme triangulaire ABC.A'B'C' a :
- La base inférieure est le triangle ABC, la base supérieure est le triangle A'B'C' ;
Les faces latérales sont des rectangles : AA'B'B, BB'C'C, CC'A'A ;
- Bords :
- Bords de base : AB, BC, CA, A'B', B'C', C'A'
- Côtés : AA', BB', CC' ;
- Sommets : A, B, C, A', B', C'.
- La hauteur est la longueur d'un côté : AA' ou BB' ou CC'.
Prisme quadrilatéral
- Un prisme quadrilatère a 6 faces, 12 arêtes et 8 sommets.
- Les deux bases sont toutes deux quadrilatères et parallèles entre elles. Chaque face latérale est un rectangle.
- Les côtés sont égaux.
- La hauteur d'un prisme quadrilatère est la longueur d'un côté.
Par exemple:
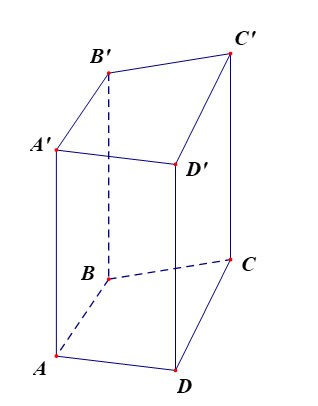
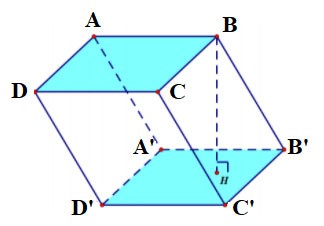
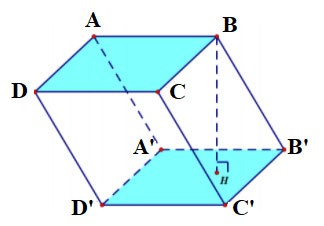
Le prisme quadrilatère ABCD.A'B'C'D' a :
- La base inférieure est le quadrilatère ABCD, la base supérieure est le quadrilatère A'B'C'D' ;
Les faces latérales sont des rectangles : AA'B'B, BB'C'C, CC'D'D, DD'A'A ;
- Bords :
+ Bords de base : AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Bords latéraux : AA', BB', CC', DD' sont égaux.
- Sommets : A, B, C, D, A', B', C', D'.
- La hauteur est la longueur d'un côté : AA' ou BB' ou CC' ou DD'.
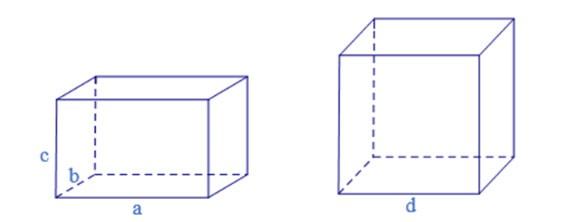
Remarque : les prismes rectangulaires et les cubes sont également des prismes quadrilatères.
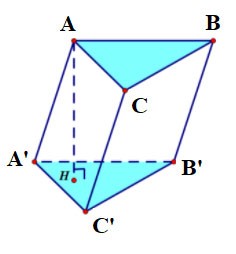
Prisme droit
Si un prisme a des bords latéraux perpendiculaires à la base, il est appelé prisme droit.
Note:
Si la base est un rectangle, le cylindre vertical du quadrilatère est appelé une boîte rectangulaire.
Si un cylindre quadrilatère a 12 côtés de longueur a, alors son nom est un cube.
Comparez le prisme droit et le prisme régulier :
| DÉFINIR: |
NATURE |
| + Un prisme vertical est un prisme dont un côté est perpendiculaire à la base. |
+ Les faces latérales d’un prisme vertical sont rectangulaires.
+ Les faces latérales du prisme sont perpendiculaires à la face de base.
+ La hauteur est le côté
|
| + Un prisme régulier est un prisme vertical dont la base est un polygone régulier. |
+ Les faces latérales d’un prisme sont toutes des rectangles égaux.
+ La hauteur est le côté
|
4. Exemple de calcul du volume d'un prisme vertical
Exemple 1 :
Étant donné le prisme ABC.A'B'C' dont la base ABC est un triangle équilatéral de côté a = 2 cm et de hauteur h = 3 cm. Calculer le volume de ce prisme ?
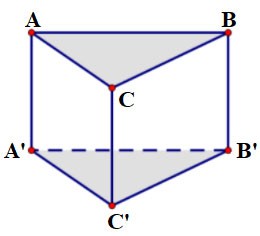
Prix:
Comme la base est un triangle équilatéral de côté a, l'aire est :
À ce moment, le volume du prisme est :
Exemple 2 :
Exercice 1 : Étant donnée une boîte verticale avec des arêtes AB = 3a, AD = 2a, AA'= 2a. Calculer le volume du bloc A'.ACD'
Instruire:
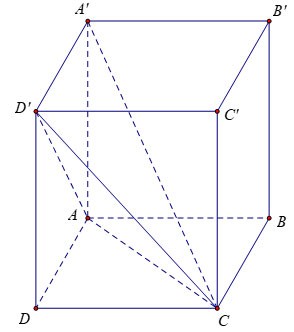
Comme la face latérale ADD'A' est un rectangle, nous avons :
Exemple 3 : Étant donné un prisme vertical ABC.A'B'C' dont la base est un triangle équilatéral de côté a√3, l'angle entre la base et le prisme est de 60º. Soit M le milieu de BB'. Calculer le volume de la pyramide M.A'B'C'.
Prix:
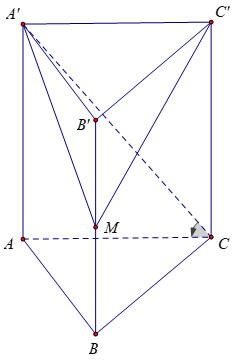
Par conséquent, nous pouvons en déduire que
Nous avons:
Exemple 4 :
Étant donné un prisme quadrilatère régulier ABCD.A'B'C'D' avec une arête de base de longueur a et une face (DBC') faisant un angle de 60º avec la base ABCD. Calculer le volume du prisme ABCD.A'B'C'D ?
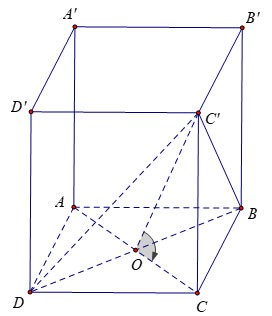
Nous avons : au centre O du carré ABCD.
D'autre part donc
Déduire
Aussi:
Exemple 5 :
Calculer le volume V du cube ABCD.A'B'C'D', sachant que AC'=a√3
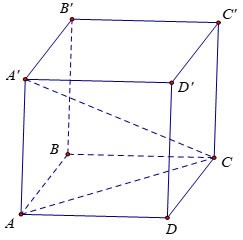
Prix:
Soit x la longueur du côté du cube.
Considérons le triangle AA'C rectangle en A avec :
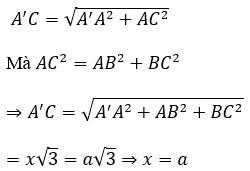
Par conséquent, le volume du cube est V=a^3.
En plus de la formule de calcul du volume d'un prisme ci-dessus, vous pouvez vous référer à d'autres articles sur la formule de calcul du volume d'un solide de révolution , la formule de calcul de l'aire et de la circonférence d'un cercle ...