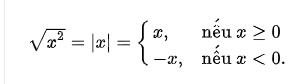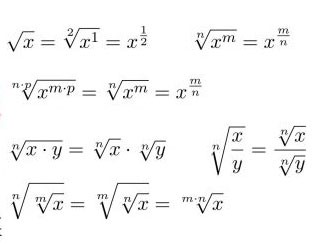La racine carrée est l’une des connaissances importantes en mathématiques utilisées tout au long du processus d’apprentissage des étudiants. L'article suivant vous présentera la définition de ce qu'est une racine carrée et comment calculer la racine carrée d'un nombre ? Veuillez vous référer à.
Table des matières
Qu'est-ce que la racine carrée ?
La racine carrée d'un nombre a est un nombre x tel que x2 = a, ou en d'autres termes, le nombre x dont la valeur au carré = a.
Par exemple, 2 et −2 sont des racines carrées de 2 car 2² = (−2)² = 4.
Le signe radical est noté √.
- Chaque nombre réel non négatif a possède une racine carrée non négative unique, appelée racine quadratique arithmétique.
Par exemple, la racine carrée arithmétique de 16 est 4, notée √16 = 4, car 4² = 4 × 4 = 16 et 4 est un nombre non négatif.
Tout nombre positif a a deux racines carrées : √a est une racine carrée positive et −√a est une racine carrée négative. Ils sont notés simultanément par ± √a.
Les calculs de racine carrée les plus élémentaires
Rappelez-vous quelques nombres carrés de base et les plus courants afin que lorsque vous prenez des racines carrées, vous puissiez calculer plus rapidement dans votre tête :
0² = 0
1² = 1
3² = 9
4² = 16
5² = 25 6² = 36
7² = 49
8² = 64
9² =
81 10² =
100
11² = 121 12²
= 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289
Voici quelques formules de base de racine carrée que tout le monde devrait retenir :
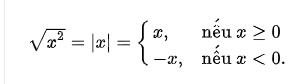
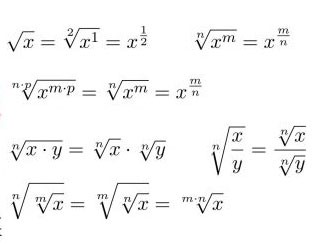
Tableau des racines carrées
Le tableau des racines carrées est divisé en lignes et en colonnes, permettant de trouver directement la racine carrée des nombres supérieurs à 1 et inférieurs à 100.
Les racines carrées des nombres écrits avec pas plus de trois chiffres de 1,00 à 99,9 sont données dans le tableau dans les colonnes 0 à 9. Ensuite, neuf colonnes de correction sont utilisées pour corriger le dernier chiffre des racines carrées des nombres écrits avec quatre chiffres de 1,000 à 99,99.
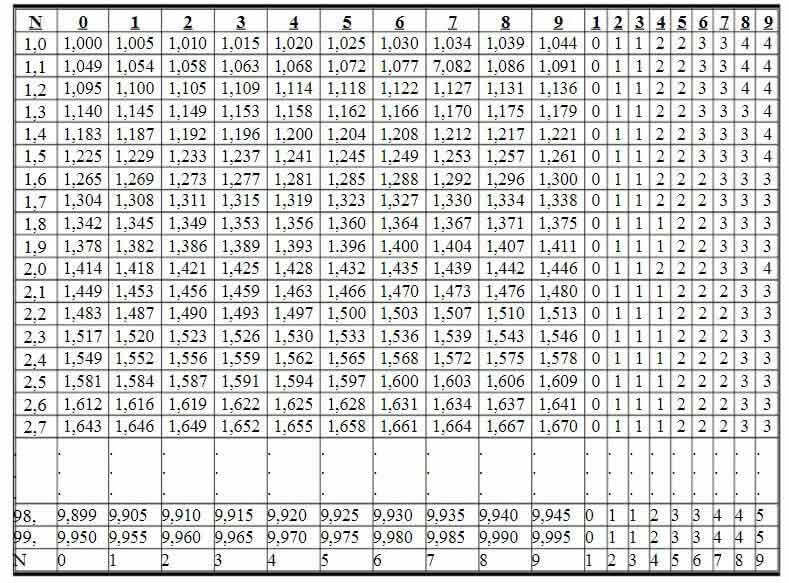
Exemple 1 : Trouver
→ Solution :
À l'intersection des lignes 1, 4 et de la colonne 1, nous voyons le nombre 1 187
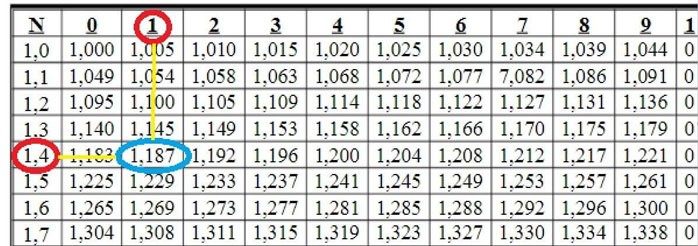
Donc
Exemple 2 :
Trouver
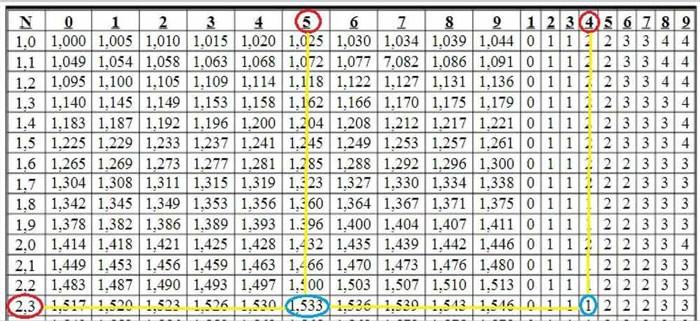
À l'intersection des lignes 2, 3 et de la colonne 5, nous voyons le nombre 1,533. Nous avons
Ensuite, à l'intersection des lignes 2, 3 et de la colonne 4, nous voyons le chiffre 1. Ce chiffre 1 est utilisé pour corriger le dernier chiffre du nombre . C'est-à-dire : 1,533 + 0,001 = 1,534
Donc
Comment calculer la racine carrée sans utiliser de calculatrice
Trouver la racine carrée d'un entier
Trouver la racine carrée par multiplication.
La racine carrée d'un nombre est le nombre qui, lorsque vous multipliez le nombre par lui-même, vous donne le nombre d'origine.
Cela signifie donc : « Quel nombre pouvez-vous multiplier par lui-même pour obtenir le nombre que vous avez déjà ? »
Par exemple:
La racine carrée de 1 est 1 car 1 fois 1 est égal à 1 (1 X 1 = 1).
La racine carrée de 4 est 2 car 2 fois 2 est égal à 4 (2 X 2 = 4).
La racine carrée de 9 est 3 car 3 x 3 = 9.
Utiliser la division pour trouver la racine carrée
Pour trouver la racine carrée d'un entier, vous pouvez diviser l'entier par des nombres successifs jusqu'à ce que vous trouviez un quotient qui soit exactement le même que votre diviseur.
Par exemple:
16 divisé par 4 est 4 donc 4 est la racine carrée de 16.
4 divisé par 2 est 2, donc 2 est la racine carrée de 4.
Trouver la racine carrée d'autres nombres
Devinez et utilisez ensuite le processus d’élimination.
Exemple : Trouvez la racine carrée de 20.
En attendant, nous savons que 16 est un nombre carré parfait avec racine carrée de 4 (4X4=16).
25 a également une racine carrée de 5 (5X5=25).
Nous supposerions donc que la racine carrée de 20 se situerait entre 4 et 5.
Nous pouvons deviner que la racine carrée de 20 est 4,5 et essayer de mettre 4,5 au carré pour vérifier. C'est-à-dire, prenons 4,5 x 4,5, si la réponse n'est pas 20, alors nous voyons si le résultat est supérieur ou inférieur à 20 pour calculer. Si c'est moins de 20, alors nous continuons d'essayer avec 4, 6 et des nombres plus grands. Si le résultat est supérieur à 20, essayez de calculer avec 4,4 et des nombres plus petits jusqu'à ce que vous obteniez le résultat correct.
Le résultat de ce calcul est 4,475 X 4,475 = 20,03. Lorsque vous arrondissez vers le bas, la réponse est 20.
Comment comparer les racines carrées
Avec 2 nombres positifs a et b
Si a = b alors
Si a > b alors
Si un < b="" alors="">
Par exemple:
Comparez et
Parce que 21 < 31,
Nous espérons que l'article ci-dessus vous a aidé à saisir les connaissances sur les racines carrées, comment calculer, comment comparer... pour résoudre des exercices sur les racines carrées ainsi que d'autres exercices connexes.