Quest-ce que lorthocentre ? Déterminer lorthocentre dans un triangle

L'orthocentre d'un triangle est l'intersection des trois altitudes , ce qui signifie que l'intersection des lignes de chaque sommet du triangle à son côté opposé forme un angle droit. La longueur de l'altitude est la distance entre le sommet et le bas.

Orthocentre d'un triangle

• Qu'est-ce que l'orthocentre ?
• Comment déterminer l'orthocentre d'un triangle
• Propriétés de l'orthocentre d'un triangle
• Exercices pour déterminer et prouver l'orthocentre d'un triangle

Qu'est-ce que l'orthocentre ?

Les trois hauteurs d'un triangle se rencontrent en un point. Ce point est appelé l'orthocentre du triangle .

Concrètement : Sur le dessin se trouvent les hauteurs, l'orthocentre du triangle.

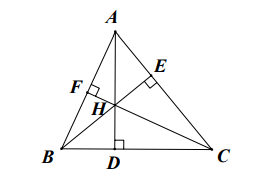
Comment déterminer l'orthocentre d'un triangle

Pour déterminer l'orthocentre d'un triangle, nous trouvons l'intersection des deux altitudes dans ce triangle.

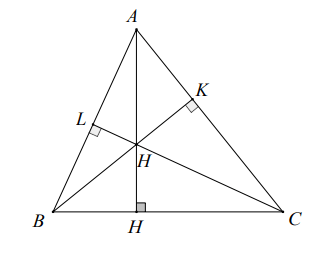
Remarque :  a) Si le triangle est un triangle aigu, l’orthocentre se trouve à l’intérieur du triangle.

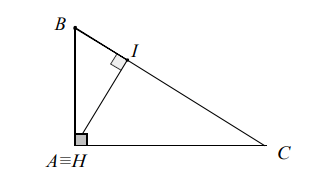
b) Si le triangle est un triangle rectangle à alors l'orthocentre coïncide avec le point .

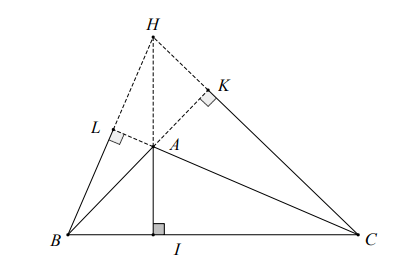
c) Si un triangle est un triangle obtus, alors l'orthocentre se trouve à l'extérieur du triangle.

Propriétés de l'orthocentre d'un triangle

Propriété 1 :  Dans un triangle équilatéral, le centre de gravité, l'orthocentre, un point équidistant des trois sommets du triangle, un point à l'intérieur du triangle et équidistant des trois côtés du triangle sont quatre points coïncidents.

Propriété 2 :  L'orthocentre coupe la bissectrice perpendiculaire de deux côtés en deux segments de longueur égale. Cela signifie que l'orthocentre est à la même distance des sommets du triangle.

Propriété 3 :  L'orthocentre est le centre du cercle circonscrit d'un triangle, ce qui signifie que si nous dessinons un cercle passant par les trois sommets d'un triangle, l'orthocentre sera le centre de ce cercle.

Propriété 4 :  L'orthocentre d'un triangle aigu se trouve à l'intérieur du triangle, tandis que l'orthocentre d'un triangle obtus se trouve à l'extérieur du triangle.

Propriété 5 :  L'orthocentre d'un triangle rectangle coïncide avec le sommet de l'angle droit de ce triangle rectangle.

Propriété 6 :  L'orthocentre est le seul point d'un triangle tel que si nous traçons des lignes allant de l'orthocentre aux sommets du triangle, la somme des longueurs de ces lignes est la plus petite. Cela signifie que l'orthocentre est le plus proche des sommets du triangle que tout autre point.

Propriété 7 : L'orthocentre est également le centre du cercle circonscrit au triangle, c'est-à-dire le plus grand cercle qui peut être tracé à travers les trois sommets du triangle.

Exercices pour déterminer et prouver l'orthocentre d'un triangle

Par exemple : étant donné un non-carré. Appelez son orthocentre. Montrez les hauteurs du triangle. À partir de là, indiquez l’orthocentre de ce triangle.

Guide de solutions

Illustration

Soient les pieds des perpendiculaires tirées de ΔABC.

Considérez ΔHBC avec :

donc AD est la hauteur de H à BC.

à F donc BA est l'altitude de B à HC

à E donc CA est la hauteur de C à HB.

se croisent en A donc A est l'orthocentre de ΔHCB.

Par exemple : étant donné un triangle rectangle de hauteur . Soit le milieu de , le milieu de est . Déterminer l'orthocentre du triangle.

Guide de solutions

Considérez le sous-problème si le triangle a et AC comme points médians respectivement alors et .

En effet, sur le rayon opposé du rayon prenons un point tel que

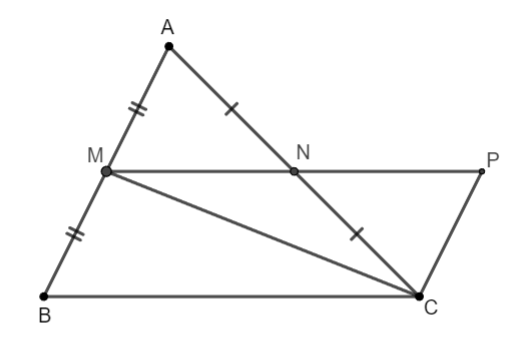
Considérons le triangle AMN et le triangle CPN.

(opposé)

, (deux côtés et deux angles correspondants)

Deux angles sont dans des positions alternées donc

=>(deux angles alternes-internes)

Considérons le triangle BMC et le triangle PCM.

(cmt)

MC est un bord commun

, (côtés et angles correspondants)

Deux angles sont dans des positions alternées donc

Nous avons encore

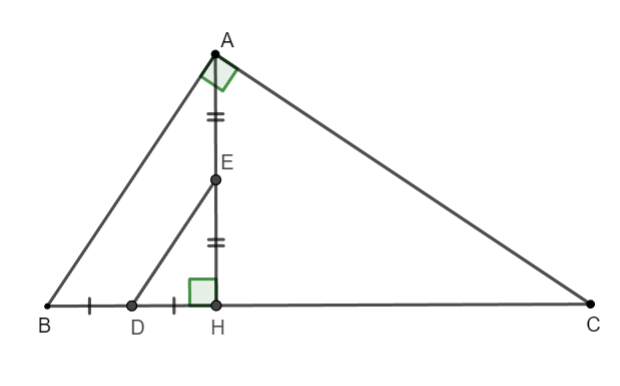
Considérons le triangle HAB avec :

(comme prouvé ci-dessus)

Considérons le triangle ADE.

d'autre part et

est la hauteur du triangle ADE

C est l'intersection du courant alternatif et du courant continu

=> C est l'orthocentre du triangle ADE

Par exemple : étant donné une échelle en A, l'altitude coupe la médiane en . Prouver et calculer ?

Instruire

Illustration

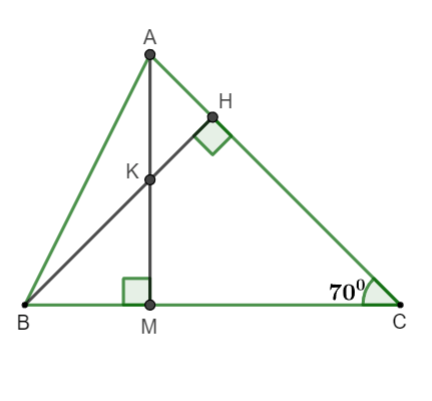
Parce que le solde est en A et AM est la médiane

⇒ AM est aussi l'altitude correspondant à BC

à M.

D'autre part, K ​​est donc l'orthocentre.

Par conséquent, K appartient à l'altitude de C de ∆ABC.

Nous avons: