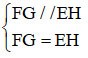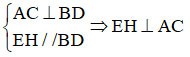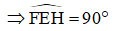Comment calculer la diagonale d'un carré, comment calculer la diagonale d'un rectangle est beaucoup utilisé dans les problèmes mathématiques et les applications pratiques telles que la conception et la construction, la coupe des coins, la mesure... Quantrimang.com a compilé des connaissances sur les propriétés de deux diagonales ainsi que des formules de calcul, veuillez vous référer à l'application dans les études, la vie et le travail.
Table des matières
Quelle est la diagonale d'un carré et d'un rectangle ?
La diagonale d' un carré ou d' un rectangle est la ligne reliant deux coins opposés. Chaque carré et rectangle possède deux diagonales de longueur égale.
Comment calculer la diagonale d'un carré
Propriétés du carré diagonal
- Les deux diagonales d'un carré sont de longueur égale, perpendiculaires et se coupent au milieu de chacune.
- Il y a un cercle inscrit et un cercle circonscrit et les centres des deux cercles coïncident et sont l'intersection des deux diagonales du carré.
- 1 diagonale divisera le carré en deux triangles rectangles isocèles.
- L'intersection des bissectrices, des médianes et des bissectrices perpendiculaires coïncide en un seul point.
- Possède toutes les propriétés d'un rectangle, d'un parallélogramme et d'un losange.
Formule pour calculer la diagonale d'un carré
Selon les propriétés d'un carré, deux diagonales d'un carré sont égales et une diagonale d'un carré divisera le carré en deux parties d'aire égale, qui sont deux triangles rectangles isocèles. Ainsi, la diagonale du carré est l'hypoténuse des deux triangles rectangles isocèles.
Ainsi, pour calculer la diagonale d'un carré, il suffit d'appliquer le théorème de Pythagore au triangle rectangle.
Supposons que vous ayez un carré ABCD de côté de longueur a, la diagonale AC divise le carré en deux triangles rectangles ABC et ACD.
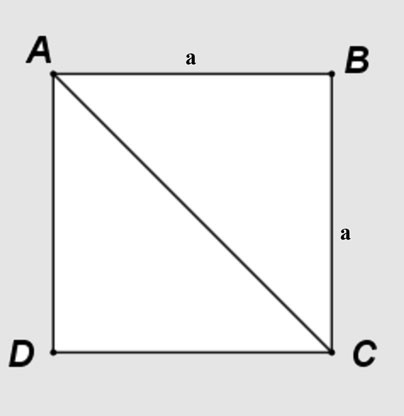
Application du théorème de Pythagore au triangle rectangle isocèle ABC :
⇒ ⇒
Ainsi, la diagonale d'un carré a pour côté a :
Exemple de calcul de la diagonale d'un carré
Exemple 1 : Un carré a un côté de 3 cm. La diagonale de ce carré est : 6 cm, √18 cm, 5 cm ou 4 cm ?
Solution:
a) En appliquant le théorème de Pythagore au carré ABC, on a :
AC² = AB² + BC² = 3² + 3² = 18
=> CA = cm
Donc la diagonale du carré est √18 cm.
Exemple 2 :
La diagonale d'un carré est de 2dm. Le côté de ce carré est : 1cm, 3/2cm, √2cm ou 4/3cm ?
Prix:
Appliquez le théorème de Pythagore au triangle rectangle ABC, mais cet exercice donne la longueur de la diagonale, soit AC = 2 cm, calculez le côté AB.
Nous avons : AC² = AB² + BC² = 2AB (car AB = BC)
=> AB² = AC²/2 = 2²/2 = 2
=> AB = √2
Comment calculer la diagonale d'un rectangle
Un rectangle est un quadrilatère convexe à quatre angles droits, c'est un parallélogramme à deux diagonales égales.
Propriétés des diagonales d'un rectangle
Les diagonales d’un rectangle possèdent plusieurs propriétés importantes qui sont utiles pour résoudre des problèmes impliquant des rectangles et leurs diagonales.
- La longueur de la diagonale d'un rectangle est l'hypoténuse d'un triangle rectangle, elle est donc égale à la racine carrée de la somme des carrés des deux côtés.
- La diagonale divise le rectangle en deux triangles rectangles d'aire égale. Ainsi, la diagonale d’un rectangle est l’axe de symétrie du rectangle.
- Les deux diagonales d'un rectangle sont égales et se coupent au milieu de chaque droite et forment 4 triangles isocèles.
Formule pour calculer la diagonale d'un rectangle
À partir des propriétés de la diagonale d'un rectangle ci-dessus, nous pouvons utiliser le théorème de Pythagore pour calculer la longueur de la diagonale d'un rectangle.
Supposons que vous ayez un rectangle ABCD de longueur a et de largeur b, diagonale AC comme indiqué ci-dessous.
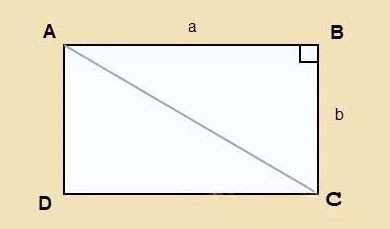
Nous appliquons le théorème de Pythagore au triangle rectangle ABC :
⇒ ⇒
Par conséquent, la diagonale d'un rectangle de longueur a et de largeur b est :
Ainsi, la longueur d'une diagonale d'un rectangle est égale à la racine carrée de la somme des carrés des deux côtés (longueur et largeur) du rectangle.
Ainsi, nous pouvons calculer la diagonale d’un carré ou d’un rectangle en appliquant simplement le théorème de Pythagore.
Exemple de calcul de la diagonale d'un rectangle
Calculez la longueur de la diagonale d'un rectangle de longueur 10dm et de largeur 5dm.
Solution:
Soit la longueur de la diagonale du rectangle a (a > 0, dm)
En appliquant le théorème de Pythagore, la longueur de la diagonale du rectangle est :
a2 = 102 + 52 = 125
=> a = 5√5 dm
Exemple pour prouver qu'un quadrilatère est un rectangle.
Les propriétés et la formule de calcul de la diagonale d'un rectangle peuvent être appliquées pour résoudre certains problèmes prouvant qu'un quadrilatère est un rectangle.
Étant donné que le quadrilatère ABCD possède deux diagonales perpendiculaires l'une à l'autre. Soient E, F, G, H les milieux des côtés AB, BC, CD, AD respectivement. Quelle est la forme du quadrilatère EFGH ? Pourquoi?
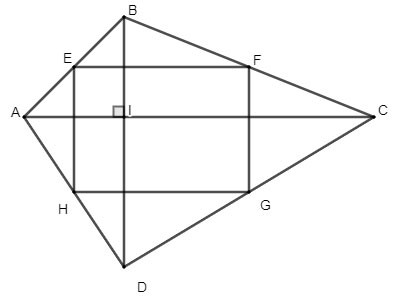
Solution:
Parce que E est le point médian de AB, H est le point médian de AD
=> EH est la médiane du triangle ABD.
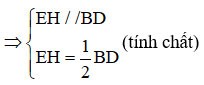 (1)
(1)
Parce que F est le point médian de BC, G est le point médian de CD
=> FG est la médiane du triangle BCD
 (2)
(2)
De (1) et (2) =>
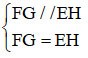
Considérons le quadrilatère EFGH.
FG // EH
FG = EH
=> EFGH est un parallélogramme (signe de reconnaissance)
D'autre part:
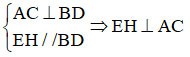
A également :
E est le point médian de AB, F est le point médian de BC.
=> EF est la médiane du triangle ABC
=> EF // AC
Mais EH ⊥ AC => EH ⊥ EF
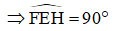
Le parallélogramme EFGH a un angle droit
=> EFGH est un rectangle




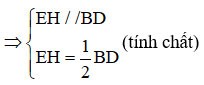 (1)
(1) (2)
(2)