Formule de calcul de la hauteur dans les triangles réguliers, isocèles, équilatéraux et rectangles

L'altitude dans un triangle est une ligne droite avec des propriétés importantes et est étroitement liée aux problèmes de géométrie plane. Alors quelle est la hauteur, comment calculer la hauteur dans un triangle ? Veuillez vous référer à l'article ci-dessous pour la réponse et la formule la plus simple pour calculer la hauteur d'un triangle.

Table des matières

• Formule pour calculer la hauteur dans un triangle
  • Calculer la hauteur dans un triangle régulier
  • Calculer la hauteur dans un triangle équilatéral
  • Formule de calcul de la hauteur dans un triangle rectangle
  • Formule de calcul de la hauteur dans un triangle isocèle
• Définition de l'altitude dans un triangle
• Propriétés des trois hauteurs d'un triangle

Formule pour calculer la hauteur dans un triangle

Calculer la hauteur dans un triangle régulier

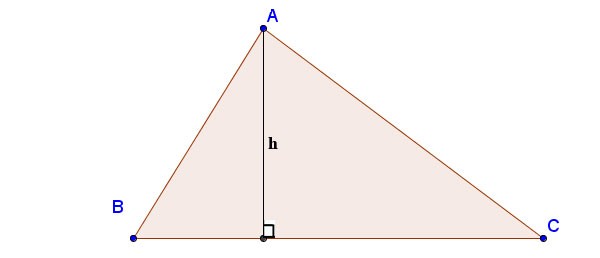
Comment calculer la hauteur d'un triangle à l'aide de la formule de Heron :

Avec a, b, c étant les longueurs des côtés ; ha est l'altitude tirée du sommet A jusqu'au côté BC ; p est le demi-périmètre :

Par exemple: 

Étant donné le triangle ABC, côté AB = 4 cm, côté BC = 7 cm, côté AC = 5 cm. Calculez l'altitude AH de A coupant BC en H et calculez l'aire de ABC.

Prix:

Demi-périmètre du triangle : P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(cm)

Hauteur   

=>

Considérons le triangle ABC, nous avons :

Donc,

Calculer la hauteur dans un triangle équilatéral

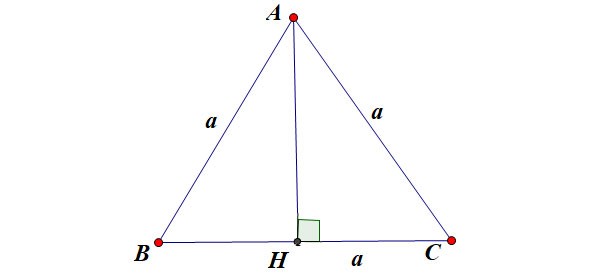
Supposons que le triangle équilatéral ABC ait une longueur de côté a comme indiqué sur la figure :

Là-dedans :

• h est la hauteur d'un triangle équilatéral
• a est la longueur du côté d'un triangle équilatéral

Formule de calcul de la hauteur dans un triangle rectangle

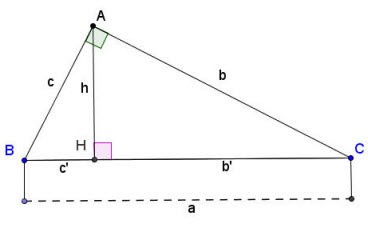
Supposons qu'il existe un triangle rectangle ABC droit en A comme indiqué ci-dessus :

Formule de calcul des côtés et des hauteurs dans un triangle rectangle :

1. a2 = b2 + c2

2. b2 = ab′ et c2 = ac′

3. ah = bc

4. h2 = b′.c'

5.

Là-dedans :

• a, b, c sont les côtés d'un triangle rectangle comme indiqué ci-dessus ;
• b' est la projection de l'arête b sur l'hypoténuse ;
• c' est la projection de l'arête c sur l'hypoténuse ;
• h est la hauteur d'un triangle rectangle tracé du sommet de l'angle droit A jusqu'à l'hypoténuse BC.

Exemple 1 : Étant donné le triangle rectangle ABC, angle A, hauteur AH. Calculez BC, AC, AH sachant que AB = 15 cm, HC = 16 cm.

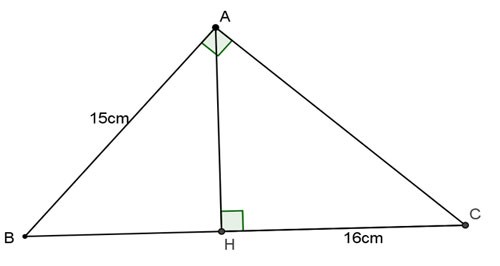
Prix:

En appliquant la formule algébrique au triangle rectangle ABC, nous avons :

AC2 = CH.BC = 16.BC

D'après le théorème de Pythagore pour le triangle rectangle ABC d'angle droit A, nous avons :

AB2 + AC2 = BC2

⇔ 152 + 16.BC = BC2

⇔ BC2 - 16.BC - 225 = 0

⇔ BC2 - 25.BC + 9.BC - 225 = 0

⇔ BC(BC - 25) + 9(BC - 25) = 0

⇔ (BC - 25)(BC + 9) = 0

⇔ BC = 25 ou BC = -9 (éliminer)

⇒ AC2 = 16.BC = 16,25 = 400 ⇒ AC = 20 (cm)

Considérons le triangle rectangle ABC avec : AH.BC = AB.AC (formule géométrique)

=> AH = AB.AC/BC = 15,20/25 = 12(cm)

Donc BC=25(cm); CA=20(cm); AH=12(cm)

Exemple 2 :

Étant donné que le triangle ABC est rectangle en A, AB = 24 cm, AC = 32 cm. La bissectrice perpendiculaire de BC coupe AC, BC en D et E respectivement. Calculer DE.

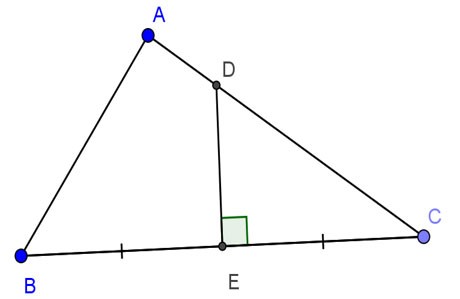
Prix:

Considérons le triangle rectangle ABC, nous avons :

BC2 = AB2 + AC2 (selon le théorème de Pythagore)

BC2 = 242+ 322

BC2 = 1600

BC = 40(cm)

CE = BC : 2 = 40 : 2 = 20(cm)

Considérons le triangle rectangle ACB et le triangle rectangle ECD avec :

Il y a ∠A = ∠E = 90o

∠C commun

=> Triangle ACB ∾ triangle ECD (gg)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15 cm

Donc ED = 15 cm

Formule de calcul de la hauteur dans un triangle isocèle

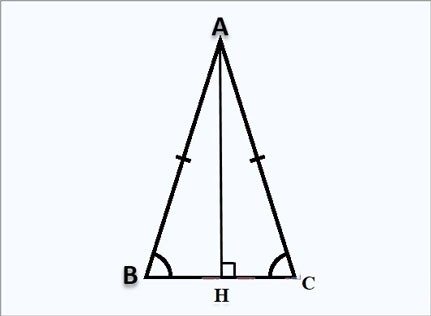
Supposons que vous ayez un triangle isocèle ABC en A, la hauteur AH est perpendiculaire en H comme indiqué ci-dessus :

Formule de calcul de la hauteur AH :

Comme le triangle ABC est isocèle en A, la hauteur AH est aussi la médiane, donc :

⇒ HB=HC= ½BC

En appliquant le théorème de Pythagore au triangle rectangle ABH droit en H, nous avons :

AH²+BH²=AB²

⇒AH²=AB²−BH²

Par exemple : Étant donné que Δ ABC est équilibré en A avec BC = 30(cm), hauteur AH = 20(cm). Calculez la hauteur correspondant au côté de ce triangle isocèle.

Solution : Considérons que Δ ABC est isocèle en A avec BC = 30(cm)

⇒ BH = CH = 15(cm).

En appliquant le théorème de Pythagore, nous avons :

Maintenant, nous devons calculer BK = ?

Nous avons:

D'autre part

Par conséquent, nous avons ⇔

Définition de l'altitude dans un triangle

Une altitude dans un triangle est un segment perpendiculaire tracé d'un sommet au côté opposé. Ce côté opposé est appelé la base correspondant à l'altitude. La longueur de l'altitude est la distance entre le sommet et le bas.

Propriétés des trois hauteurs d'un triangle

Les trois hauteurs d'un triangle passent par le même point. Ce point est appelé l'orthocentre du triangle .

Il vous suffit de calculer les composants inconnus dans les formules ci-dessus pour calculer la hauteur d'un triangle pour pouvoir calculer la hauteur d'un triangle.

• Quel est l'objectif ? Formule de calcul du centre de gravité d'un triangle